Introduction
Data mining is part of a process known as knowledge extraction (KDE), which appeared in the scientific community in the 1990s. It is a fast-growing research field aiming at exploiting the large quantities of data collected every day in various fields of computer science. This multidisciplinary field is at the crossroads of different domains, such as statistics, databases, big data, algorithms, and artificial intelligence. The type of data mining algorithm varies according to the type of data (binary, categorical, numerical, time series, spatial, etc.) of the dataset on which the algorithms will be applied, or the type of relationship between the patterns searched (sequence, co-variation, co-occurrence, etc.) as well as the level of complexity and semantics of the analyzed data (1). It is generally about finding co-occurrences or dependencies between attributes or items and relationships between objects or transactions in the dataset, unlike clustering, which is used to find relationships between objects. Gradual and maximal pattern mining, discussed in this article, is part of the search for frequent gradual dependencies between attributes of the dataset (2). Since automatic KDE has to be performed in large volume databases, empirical studies already show that at the level of generalized patterns, association rules, and frequent gradual patterns, one has to exponentially increase the size of the search space to be explored in order to extract useful knowledge. To make better decisions in real life and to refine the analysis of domain experts in a reasonable time, the authors have developed many algorithms to solve these problems of search space reduction and better CPU and memory performance. Nevertheless, very few works offer the final customers a reduced number of relevant patterns extracted. Thus, the technique of mining closed gradual patterns was developed (3). The goal is to extract a condensed representation of fuzzy gradual patterns based on the notion of closure of the Galois correspondence. It is used as a generator of rules and gradual patterns. We can cite other classes of algorithms based on multicore architectures that minimize the extraction time compared to their sequential versions. We find, in particular, the work of Negreverge with his Paraminer algorithm (4), the pglcm of Alexandre Termier. However, very few works are oriented on the extraction of frequent and maximal gradual patterns. The specificity of this work is the use of a hybrid approach of dataset partitioning and SGrite-based.
Objectives
General objective: Extract frequent and maximum gradual patterns from big database
Specific objective 1: Our algorithm relies, on the one hand, a reduction of half in the first step of the research space; by using as a search space, the lattice has at least one positive term. Two simultaneous traverses of the above mentioned lattice are performed: an ascendant constructs the candidate sets of size 1 to a size k, k < n, where n is the total number of items. During the browse, SGrite join is used, and the other descendants manage the maximum gradual candidates and frequencies. This objective is the exploitation of the lattice with at least one positive term as well as a two-way lag with a view to further reduce the operations of calculation of the support and thus the search space.
Specific objective 2: Guarantee extraction in large databases
Observing the degree of memory saturation during gradual pattern discovery using Grite, SGrite, and Graank methods has involved preprocessing to reduce the dataset size (5) in the case of very correlate or dense data. This adaptation is necessary to carry out the extraction. However, this search remains partial and can lead to the loss of quality patterns; indeed, certain co-variations between the attributes considered in the original dataset and the rest of the dataset ignored remain unvalued. To partially solve this problem, we propose to process a search by partitioning the dataset, which will be described in section “Presentation of the Hybrid Extraction Method for Maximal Gradual Patterns.”
Literature review
Definitions
Definition 1. Gradual item (1, 5–8): It is an attribute. A provided with a comparison operator * ∈ {≤, ≥, <, >} that reflects the direction of variation of the values for this attribute A. It is noted as A*. If * is equal to ≥ (resp. ≤), then A* captures an increasing (resp. decreasing) variation of the values of A.
For example, A≥, A≤, and S≥ are gradual items induced by Table 1. They are interpreted as “the more age increases,” “the more age decreases,” and “the more salary increases.”
Definition 2. Gradual itemset (5–10): A gradual itemset, denoted by {(Ai*i),i = 1…k} or {Ai*i, i = 1…k}, is a set of gradual items that expresses a co-variation of the considered items. This set is interpreted semantically as a conjunction of gradual items.
For example, the gradual itemset A>S< deduced of Table 1 means that “the more age, the less salary.”
Definition 3. Complementary gradual pattern (1, 5, 9): If a gradual pattern M = {(Ai*i), i = 1…k}, then its complementary gradual pattern of the same size is denoted c(M). It is defined by c(M) = {(Aic(*i)), i = 1…k}, where c(*i) is the complement of the comparison operator *i.
Note: In the previous works (1, 5), c(≤) = ≥, c(≥) = ≤, c(<) = >, c(>) = <.
In Table 1, for example, two gradual patterns A> and A>S< are considered; their complementary is the gradual patterns A< and A<S>.
Definition 4. Inclusion of gradual patterns: The gradual pattern X is included in the gradual pattern Y, noted as X ⊆ Y, if all the gradual items of X are also present in Y.
For example, from Table 1, the gradual pattern A>S> is included in the gradual patterns A>S>V> and A>S>V<.
From definitions 3 and 4, we can deduce the two properties allowing a significant pruning of the search space. The first property is the equality property of gradual support (1, 5, 11) and the second is the anti-monotonicity property of gradual support (1, 5, 10, 11).
Definition 5. Lattice of gradual patterns (5). A lattice of gradual patterns is a lattice induced by the set of gradual patterns provided with the inclusion relation. The set of nodes of the lattice is the set of gradual patterns. An arc that goes from a gradual pattern A to a gradual pattern B reflects the inclusion of A in B.
Definition 6. Lattice of gradual patterns with first-term positive: It is a sub lattice of the lattice of gradual patterns that only has as a component the gradual patterns of which at least the first gradual item of each component is positive. They are noted on the form {Ai*i }, i = 2…k.
The lattice of gradual patterns is the search space of frequent gradual patterns which is halved by the lattice with the first positive term. To illustrate our point, let us take, for example, Figures 1, 2.
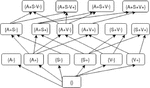
Figure 2. Lattice of gradual patterns with first-term positive obtained from the items of Table 1.
Gradual pattern mining approaches
The linear regression technique described by Huller-Meier (12) allows for the extraction of gradual dependences with more support and confidence than the user-specified threshold. This method only takes into account fuzzy data and rules with premise and conclusion numbers less than or equal to two. However, the T-Norm idea, which is part of this technique, allows us to transcend the size restriction of the premise and the conclusion of the rules. The weight of a gradual pattern, also known as Gradual Support (SG) in the method of Berzal et al. (13), is equal to the number of pairs of distinct objects that verify the order imposed by the pattern divided by the P total number of couples of different objects in the database. Thus, , where M is a gradual pattern and D is the database.
Laurent et al. (10) expand on the technique of Berzal et al. (13), which utilizes the fact that if a pair of objects (o, o’) validates the order established by a gradual pattern, the pair (o’, o) does not.
The gradual support of a gradual pattern M is equal to the length of a maximal path associated with M divided by the entire number of datasets in the so-called maximum pathway approach (9, 11, 14, 15). In this method, we have .
Grite serves as the foundation for the SGrite (5, 16) methodology. It prunes the search space by utilizing the support’s anti-monotonicity and complementary patterns properties. The lattice with the first-term positive utilized reduces the search space by half. Another difference between SGrite and Grite is that SGrite only takes one sweep of the dependency graph to compute gradual support, whereas Grite requires two sweeps. She employs two types of gradual support computing algorithms, each of which does a single sweep of the precedence graph.
The SGrite algorithm
The two main activities in the SGrite algorithm are the creation of candidates and the computation of the support. As it is run for each candidate, the support calculation is the most requested and CPU-intensive procedure. The SGrite algorithm is built on the following notions. In the definitions that follow, O is the set of objects, and o and o’ are objects.
Definition 7. Adjacency matrix: The adjacency matrix of a gradual pattern M is a bitwise matrix that assigns the values of 1 to every pair of objects (o, o’) if the pair of objects satisfies the pattern M’s order and 0 otherwise.
A pattern’s adjacency matrix generates a dependence graph with nodes that are objects, and nonzero adjacency matrix inputs reflect the dependencies between pairs of nodes.
Definition 8. Father node and son node: Given a pattern M’s adjacency matrix AdjM, for AdjM[o, o’] = 1, we translate the fact that o is the father of o’ and o’ is a child of o.
Definition 9. Isolated node: It is a node that is not linked to another node, i.e., it does not have a father or a son. Considering a pattern M’s adjacency matrix AdjM, the set of isolated nodes is defined by: {o ∈ O| ∀o’ ∈ O, AdjM[o, o′] = 0 ∧ AdjM [o′, o] = 0}.
Definition 10. Root: It is a node that has no parent but is connected to all the other nodes. For the model M’s adjacency matrix AdjM, the root node-set is formally defined by {o ∈ O| ∀o’ ∈ O, AdjM[o, o′] = 1 ∧ AdjM [o′, o] = 0}.
Definition 11. Leaf: It is a node that does not have a son but is not isolated. Given a pattern M’s adjacency matrix AdjM, the leaves node-set is formally defined by {o ∈ O| ∀o’ ∈ O, AdjM[o, o’] = 0 ∃o″∈ O∣AdjM [o″, o] = 1}.
The SGrite algorithm accepts an adjacency matrix, an object node ∈ O, and a vector of size | O| whose indexes are the objects of O as input. Before running each algorithm, we assume that ∀o ∈ O, Memory[o] = −1. Memory[o] holds the current maximum distance between o and any leaf throughout the execution of each algorithm. Memory[o] holds the ultimate maximum distance between o and any leaf at the end of each algorithm’s execution. The first class of algorithms updates the values of a node’s parents whenever the value of this node changes. The second class of algorithms uses just the final value of a node to update the values of his parents’ nodes. We have four different variants of the SGrite method, namely, SGOpt, SG1, SGB1, and SGB2 (5).
Methodology
To achieve our goals, several properties must be considered: (P1) anti-monotony support, (P2) complementary gradual patterns, and (P3) use of the frequency of sub-patterns of a frequent gradual maximum for pruning. The role of P1 and P2 is already known and shown in SGrite for the upward traversal for the generation of frequent gradual patterns. P3 makes it possible in the downward traversal to ignore frequent gradual sub-patterns of a maximal gradual pattern that I have to determine in advance. At the same time, during the extraction process, in the downward path of the lattice with at least one positive term, we construct the maximal progressive candidates, which belong to the lattice, with at least one positive term, hence, the guarantee of the conservation of the properties of the optimal search space. In addition, by browsing down, we can reduce the search space further by chain filtering. Thus, we use to prune, on the one hand, the set of infrequent gradual sub-patterns which is applied to the maximal gradual candidates, and, on the other hand, the sub-patterns of a frequent and maximal gradual pattern discovered beforehand starting from a set of the candidate gradual maxima of larger size during the procedure, and finally, the last pruning is done by calculating the gradual support to check the frequency of the candidates and their relevance. To complete the extraction process, there are two stop conditions. Either the current set of candidates is exhausted during the upward traverse, or the maximum number of candidates is exhausted first and the search is also terminated.
Hypotheses
1. Global time reduction of the support computation (the one brought by SGrite, omission of the computation of the gradual support of the frequent sub-patterns, and the reduction of the depths of the dependency graphs associated with the maximal candidate pattern), following the computation of the fusion of the n gradual items composing the candidate in question.
2. Reduction of the search space.
3. The reduction in the number of gradual knowledge produced, but with the possibility of listing them exhaustively.
4. The choice of the size of the different partitions. To begin, we take 2 partitions, and we also take partition 1 the biggest possible extractable by SGrite, and then partition 2 is a supplement of items of the considered dataset.
Presentation of the hybrid extraction method for maximal gradual patterns
In this section, we will explain the general operating principles of the MPSGrite method. Section “Partition Working Principle” explains how the partitioning method works. Section “Principle of Finding Maximum Gradual Patterns” presents the operation of the algorithm for finding maximum frequent gradual patterns. The notations used in this part are summarized in Table 4. It is important to specify that what motivates this algorithm is its relevance. Indeed, the algorithm is oriented toward a different concept from that of “SGrite” and its extensions; partition will have the particularity of being much more efficient on very large databases, like the current OLTP1 systems, hence, the importance of his study.
Partition working principle
To simplify the description, we will limit 2 partitions and consider a dataset D, which has n items. D is partitioned into two datasets D1 of size n1 and D2 of size n2, such that n = n1 + n2. D1 represents partition 1 of the database containing the n1 first items, while 2 is the second partition containing the n2 last items of D.
Definition 12. Partition of a database: It is a part of D which has the same number of transactions as D and which takes a contiguous subset of the items from the dataset D representing the items taken into account in the score. Being denoted by D and I = {ik} k = 1…n the items, nk < n, if Dk the kth partition that starts with item number l/l = l < n, we have Dk = (O,I) with I ⊆ I and I = {ik}k = l…l + nk–1.
Definition 13. Independence of two partitions of a database: Let D1 = (O, I1) and D2 = (O, I2) be two partitions of a dataset D = (O, I) / I1 ⊂ I, I2 ⊂ I. They are independent iff I1 ∩ I2 = Ø.
Example 14. Illustration of partition
Let I = {A, S, V} be the set of attributes of the salary dataset (see Table 1) where A is the age attribute, S is the salary, and V is the vehicle location number attribute.
For example D1 = (O,{A, S}) and D2 = (O,{V}) are two independent partitions of dataset of Table 1.
Order defined on the sets.
Definition 15. Order on items: The order relation on the set of items of a dataset D, denoted by <I, denotes the natural order relation of appearance of items in D.
For example, in the dataset of Table 1, we will have an order between the items A < I S < I V.
Definition 16. Ordered gradual itemset: An ordered gradual itemset is a gradual itemset that respects the set of items that constitutes the order defined by its position in the set of items for the dataset D = (O, I) considered. Being denoted by M = {Ai*i }i∈{1,2,…,n} a gradual k-pattern, it is ordered iff ∀j, 1 = j < k, where j represents the index of appearance of the item in the pattern M, and we have Aj <I Aj+1.
Definition 17. Gradual positive ordered itemset: A positive ordered gradual itemset is an ordered gradual itemset so atleast the first term has increasing variation.
For example, the gradual itemsets A > S < , A < S < , A > V < , and A < S < V < are ordered gradual itemsets. In con- trast, S < A > is not an ordered gradual itemset, even if it has the same meaning and the same gradual support as A > S < ordered.
Proposition 18. Total order on two gradual items: When doing a pairwise comparison of gradual items, for example, and , if A1 < I A2, then and vice versa, but in the case of A1 is equal to A2, the order is induced by the variation associated with each gradual item as follows: if *1 = *2, then ; if, in contrast, *1 = < and * 2 = > , then , so if *1 = > and * 2 = < , then .
For example, in Table 1, S < S >.
Definition 19. Order on two gradual ordered patterns: Let M1 = { A1i*i }i = 1…k1, M2 = { A2i*i }i = 1…k2 such that k1 = k2 two ordered gradual itemsets (see Definition 16). They are ordered iff ∀k = 1…min(k1, k2),A1k < I A2k or A1k*k < m A2k*k (see Proposition 18). Note this order relation between ordered gradual patterns < mI wethenhaveM1 M2.
For example, for the gradual itemsets A > S <, A > V < respects the following A > S < A > V <, which means that the gradual pattern A > S < is less than A >V < following this order relation.
Definition 20. Set of ordered gradual patterns: It is a set of gradual patterns ordered by the relation . Being denoted by LMgO = {Limgo}i = 1…n the set of sets of ordered gradual patterns ∀Limgo ∈ LMgO such that Limgo = {mj }j = 1…k, then we have ∀mj, mj+1 e Limgo, mj mj+1, with j = 1…k −1. Each Limgo is a set of ordered gradual patterns.
Principle
The search by partitioning is based on the principle of SGrite, that is to say, one of these optimal variants SGOpt or SG1 (5) on each of the independent partitions considered. Once all the sets of frequent patterns of each of the partitions have been determined and organized by level, according to the sizes of patterns, we must initially merge the gradual patterns of the same level of each partition. The next step is to generate the missing potential candidates by the method described below. This process of determining the frequencies of the whole database goes from a frequent item set of size 1 to the maximum possible size. The steps below always take place in the search space for the lattice at the first positive term. We can summarize the approach in 4 steps:
1. Step 1: determination of the frequent and infrequent gradual patterns of each partition;
2. Merging, level by level, of the gradual itemsets of all the partitions, on the one hand, the frequent ones and, on the other hand, the infrequent ones;
3. Iterative and pairwise generation of candidate patterns, based on the gradual patterns determined in step 2 as follows:
(a) Choose two levels to start the generation of gradual candidates of size k + 1 from the frequency of size k previously known. The start level and next level are, respectively, 1 and 2;
(b) For each candidate c k = {A1*ii = 1…k}, frequent, of the current ordered set of the gradual patterns consider’s of size k, extract its prefix, Prefixk-1 = { A1*i i = 1…k−1 }.
(c) From the obtained prefix, construct its adjacency matrix, and find the bounds in the set of ordered frequent and infrequent gradual patterns of size k having as prefix, Prefixk–1;
(d) Then, retrieve the value of maximum attribute, noted as max. It is the gradual item in position k, resulting from the two sets of size k (frequent and infrequent) which has the greatest value;
(e) Generate the suffixes that are used for the merge with Prefixk–1, and noted IGc = {(max + i) <, (max + i) >}i = 1…(| I| –max+1) of gradual items.
(f) Determine support for new candidate’s c new = Prefixfc–1 ∪ e, ∀e ∈ IGc. The frequents are added to the frequent gradual k-patterns of level k and the infrequent to the in frequent gradual k-motfs.
(g) Repeat the process 3-(a) to 3-(f) until the set of frequently ordered graduals of size k is exhausted.
4. Repeat steps (2) and (3) until the current candidate se is empty.
Illustration of partition
Example 21. Step 1: collection of frequent gradual pattern by each partition.
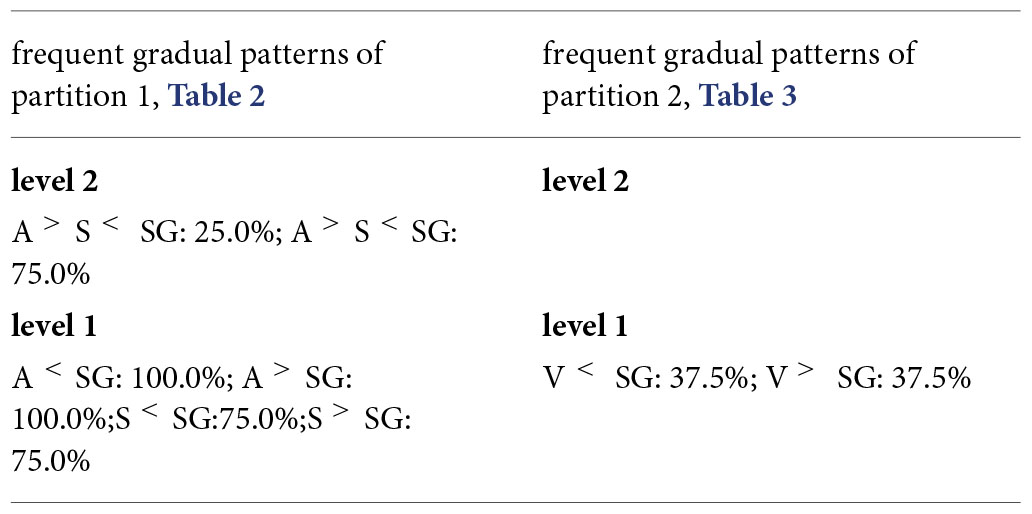
Example 22. Step 2: merge the gradual patterns from partitions 1 and 2 (see Tables 2, 3).

Example 23. Final step: Set of frequent gradual patterns of all partitions.
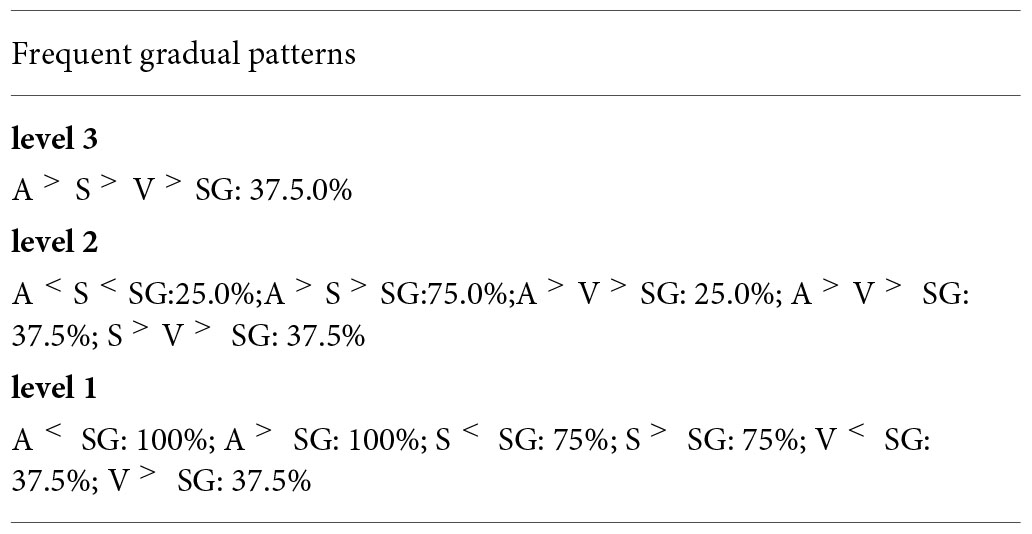
In this phase, we can see that in the gradual 2-patterns those in red color are generated by new patterns formed from items of the 2 partitions.
Example 24. Collection of frequent gradual patterns of Sgrite method.
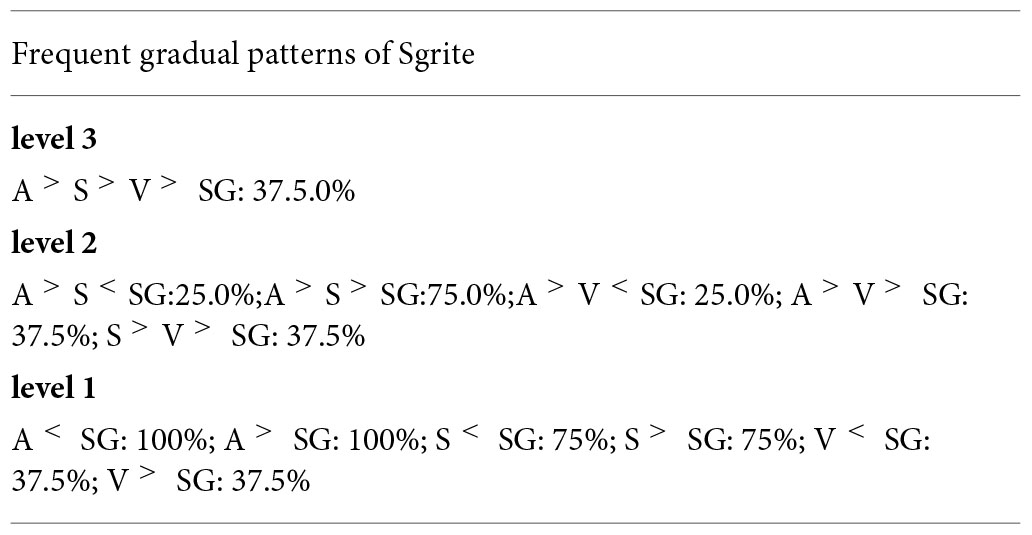
In the abovementioned notations, the sets mapCG and IFkG all have the two fields: gradual pattern and gradual support(SG), for each of the elements belonging to these sets. The sets mapFr, mapFG, mapCG, mapIFr, and mapI FG are maps or association tables where the keys are sizes of gradual patterns of each level and the values are a set of k-gradual patterns ordered by the level k considered (i.e., of key k).
Remark: all sets of gradual itemsets contains the positive ordered gradual itemsets.
● The Partition-Gen-Sgrite (Dr, minSupport) algorithm uses the SGrite principle on Dr and returns the set mapFr local gradual frequent patterns, i.e., gradual patterns ordered according to the definition 20 which are frequent in the partition Dr range by frequency size level. It updates, during the traversal of each level of the lattice with at least one positive term, the infrequent gradual patterns of the abovementioned level in the set mapIFkr from mapIFG.
● The procedure genCandidateFreqUnionTwoPartition Consecutive (Fp1, Fp2, mapFG, and mapIFG) allows to generate and update the set of global frequent and infrequent candidates obtained from the sets Fp1 and Fp2 here partitions being processed.
In algorithm 2, the data structure resultatR has five fields: type Map which represents the indicator on the set choose between mapFG and mapIFG, where we will find the gradual item index value of the suffix of the level pattern prefix, Prefixlevel maximal; min1 and max1 are the index bounds of over-patterns of Prefixlevel in mapFlevelG+1; min2 and max2 are the index bounds of the over-patterns of Prefixlevel in mapIFGlevel+1. The construction of resultatR is carried out using the function byPrefixFindPositionsMinMax of algorithm 2. The function matrixAdjacency determines the adjacency matrix of the gradual pattern taken as a parameter. The genCandidatOfALevel function generates candidate patterns of size level + 1, following the principle described in step 3-(e) of Section “Partition Working Principle.” In this algorithm, on line 1, the productCartesian function generates a set of patterns resulting from the Cartesian product of the two sets taken as a parameter; here, [get(Fkpii)] [resp. get(Fkpii)] represents the ordered set of the gradual patterns of the level ki of mapFpi(resp. the set of gradual patterns complementary to each pattern of level ki of mapIFpi).
The function filterSetByInfrequentSetAndSupportCompute (candidateFusion) allows: (1) to prune first the candidates of its set candidateFusion in parameter, which are supermotif of a inferred pattern of mapIFG. If the candidate to prune is Ck = {Ai}i = i…k then it generates two new candidates of size k −1, C1k –1 = {Ai }i=1…..k –1, C2k–1 = {Ai}i = 1…k–2 U Ak which are added to the potential candidate list. On the other hand if C k is frequent then, we add Ck at level k of mapFG and its two frequent sub-patterns C1k–1, C2k–1 build exactly as above at level k−1 of ma pFG. Once candidateFusion = 0 we have completed the process (1) and we have a valid candidate set list. Second, in (2) we have to perform another filtering by support calculation. Here, for any candidate k-pattern Ck = {Ai}i = 1…k of list, Ck ∈ list: if Ck is frequent then we add Ck at level k of mapFG, and C1k–1, C2k–1 at level k–1 of mapFG, otherwise delete C k of list and add at the end of the list C1 k–1, C2 k–1 as a new candidate in the list. We repeat this process until list = 0.
Note: In each of the algorithms below, before calculating the support of a k-pattern, we check if it does not belong to one or the other sets ma pFkG or mapIFkG, because indeed the k-pattern may well have been determined during the ascending scan of the search space of the trellis to the first positive term or during the descending scan. The interest is to reduce the number of support computations to the maximum which is a greedy operation.
Principle of finding maximum gradual patterns
The method we use is based on SGrite, which itself is an optimized method of Grite in terms of CPU time for extracting gradual patterns. Indeed, the MPSgrite method that we developed in this article has two objectives to achieve. The first objective is to optimize the time for extracting the gradual patterns considered, and the second goal is to reduce the number of gradual patterns extracted. Indeed, in real life, experts in the field say that the fewer patterns extracted, the easier it is to interpret and make decisions. We first opt for an approach of dual traversal of the lattice space to the first positive term from levels 1 to n by SGrite and simultaneously from levels n to 1. The first problem of this combined approach is the generation of the candidates of the maximal set which is of the order of 2n–1, with n the number of gradual items of the database. Consequently, the generation of candidates will have a higher CPU time cost. In addition, we also note that:
Lemma 25. The greater the number of maximum initial candidates, the higher the determination of the following maximal candidate sets, as well as the operation of fusion of n adjacency matrix composing the n-candidate gradual motifs considered.
Thus, to keep an optimal method of extracting the gradual patterns of the abovementioned maxima, it will be a question of opting for a hybridization method. The base will be based on the choice to be made according to the parameter n number of gradual items. Dataset D of n items, t transactions, and a fixed value p are considered, representing which method to use. Under these conditions, if n is less than or equal to p, then MPSGrite uses the two-way browse method sense, that is, simultaneously ascending and descending from the lattice to a positive term. On the contrary, if n is strictly greater than p, then a bottom- up lattice traversal approach is used which first efficiently generates the lattice of frequent gradual patterns, and then conversely in the descent of the lattice, by “backtracking,” we extract the frequent and maximal gradual patterns.
Presentation of the components of the hybrid method
The search space is limited in each of the components below to the lattice with a positive term. Two components of the hybrid method are required, namely, component 1 and component 2. Component 1 takes place following the path in two simultaneously ascending and descending directions of the positive lattice, and its description is carried out in section “Presentation of the Hybrid Extraction Method for Maximal Gradual Patterns.”
Component 2: Ascending the positive lattice
This algorithmic component proceeds in two main steps: In step 1, it is a question of extracting the frequent gradual patterns performed by SGrite. Once this first step is completed its result will be an entry for step 2.
In step 2, we generate the maximum gradual patterns from the frequencies of step 1. During the generation, we must respect the notion of lexicographic order of Apriori, Grite, and SGrite. Let m = n is the size of frequent gradual patterns of maximum cardinality.
Algorithm 1. genCandidateFreqUnionTwoPartition Consecutive.
begin:
Require: Fp1; Fp2; mapFG; mapIFG;
Ensure: ma pFG; mapIFG;
{fusion of the frequent patterns of the
highest level of the 2 partitions of
level k1 and k2}
1: candidateFusion←productCartesian
, U ); {Filtering
of candidates: pruning of over-patterns
of infrequents and infrequents
determined by calculation of the
support}
2: while candidateFusion ≠ Ø do
3: candidateFusion = filterSetByInfre
quentSetAndSupportCompute
(candidateFusion);
4: end while
{initial reference level for the lattice
path};
5: level = 1;nextLevel = 2;k = k1+k2;
6: refList←mapFGlevel;
7: while level ≤ length(mapFG)−1 and
nextLevel ≤ length(mapFG) do
8: for j = 1 to length(refList) do
9: Prefixlevel ← get(j, refList);
10: resuitatR = byPrefixFindPositionsMin
Max(mapFG, mapIFG
Pre fixlevel, nextLevel);
11: adjPrefix = matrixAdjacency(Prefixlevel);
12: genCandidatOfALevel(mapFG, mapIFG,
resultatR, adjPrefix, Prefixlevel,
nextLevel); adjPrefix, Prefixlevel,
nextLevel)
13: end for
14: level← level + 1;
15: nextLevel nextLevel + 1;
16: refList = ← mapFGlevel;
17: if not∃mapFGextLevel then
18: putToMap(mapFG, nextLevel,∅);
19: end if
20: end while
21: return (mapFG, mapIFG)
In this case, the set of the so-called frequent maximum is initialized by all the frequent gradual m-patterns. Then, one proceeds iteratively to prune the level k−1 of all the subpatterns which allowed the construction of the maximum gradual k-patterns previously determined and purified at iteration k. This process continues in this way until the current processing value of k is 1. In fact, when k = 1, the maximum 1-gradual patterns are determined. This completes the “backtracking” determination of the maximum step patterns.
Experimentation
This section experimentally compares the performance of SGRrite and the novel hybrid approach MPSGrite. We used three sets of data. The first two are test data called F20Att100Li having 20 attributes and 100 transactions and F20Att500Li having 20 attributes and 500 transactions (5). The last set of data is made up of meteorological dataset. For further experimentation, we have added five other datasets: a test dataset that is C250-A100-50 and 4 other real ones that are Life Expectancy developed, Life Expectancy-developing, wine quality-red, and fundamental.
Description of the datasets
This part presents the data used for the experiments carried out in this work.
We used a practical database called the weather forecast downloaded from the site http://www.meteo-paris.com/ile-de-france/station-meteo-paris/pro/. The dataset comprises 516 practical data recorded over two days (July 22–23, 2017), which are defined by 26 real numbers including temperature, cumulative rain (mm), humidity (percent), pressure (hPa), wind velocity (km/h), wind perceived temperature, or wind distance traveled (km) (5).
The C250-A100-50 dataset is taken from the site https://github.com/bnegreve/paraminer/tree/master/data/gri. For the reason of memory space, we have reduced the initial number of items from 100 to 12, because, otherwise, the extraction is not possible on our computer.
Winequality-red dataset is taken from the site https://archive.ics.uci.edu/ml/datasets/wine+quality. It is the Wine Quality dataset related to red vinho verde wine samples, from the north of Portugal. The goal is to model wine quality based on physicochemical tests. The dataset’s attributes make use of the following items: volatile acidity, citric acid, fixed acidity, residual sugar, free sulfur dioxide, total sulfur dioxide, density, pH, sulfates, alcohol, and quality (based on sensory data) (scores between 0 and 10).
These two datasets LifeExpectancydevelopped.csv and LifeExpectancydevelopping.csv (5) are also the real datasets taken for the site https://www.kaggle.com/kumarajarshi/life-expectancy- who that are open-access data. The data were as collected from the World Health Organization (WHO) and the United Nations website with the help of Deeksha Russell and Duan Wang. For this life expectancy dataset, attributes 1 and 3 are removed and the rest are used (5). The dataset is designed to answer some key questions such as: do the different predictors I initially select actually affect life expectancy? Should countries with low life expectancy (under 65) increase health spending to increase life expectancy? Is life expectancy related to diet, lifestyle, exercise, smoking, alcohol etc.? Is there a positive or negative relationship between life expectancy and alcohol consumption? Do densely populated countries have a lower life expectancy? How does immunization coverage affect life expectancy? The final merged file (final dataset) consists of 22 columns and 2,938 rows or 20 predictors. All prognostic variables are immunization factors, mortality factors, economic factors, and social factors. Due to the size of the original dataset, we split the data into two groups: LifeExpectancydevelopping.csv for developed countries and LifeExpectancydevelopping.csv for developing countries, where we removed transactions with values empty.
The fundamentals.csv dataset contains metrics extracted from annual SEC 10K fillings (2012–2016), which should be enough to derive most of the popular fundamental indicators. The fundamentals.csv comes from Nasdaq Financials. For this dataset, we have at the beginning 77 attributes. After preprocessing which consisted of removing empty- valued transactions, we derived a dataset with 1,299 transactions and 74 attributes. The removed attributes are the first four: stock symbol, end of period, accounts payable, and accounts receivable, for more information, see https://www.kaggle.com/dgawlik/nyse?select=fundamentals.csv; for reasons related to the characteristics of our small memory computer, we extracted part of the fundamental.csv dataset for the experiments, which gave us a dataset of 300 transactions and 35 attributes. Transactions are the top 300 and attributes are the top 35 (5).
Evaluation of algorithms
All tests on the datasets presented in the preceding part were performed on an Intel Core T M i7-2630QM CPU running on 2.00 GHz × 8 with 8 GB main memory and Ubuntu 16.04 LTS. We investigated a number of support levels for each dataset and measured the associated execution times (shown in Figures 3, 5, 8, 10, 12, 14, 16, 18), as well as the number of retrieved patterns (shown in Figures 4, 6, 9, 11, 13, 15, 17, 19). In these figures, (N It. X M Tr.) represents the number of items (N) and transactions (M) inside the dataset.
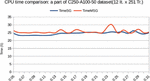
Figure 3. Different CPU times [Tr. (Resp. It.) denotes transactions (resp. Items)] dataset C250-A100-50, 251 Tr. et 12 It.

Figure 4. Experimentation on dataset C250-A100-50 for the number of patterns gradual extracted. (A) Experimentation 1 data set C250-A100-50. (B) Experimentation 2 data set C250-A100-50.
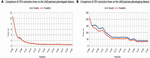
Figure 5. Different CPU times [Tr. (Resp. It.) denotes transactions (resp. Items)] for life expectancy. (A) Data set life expectancy developed, 245 Tr. et 20 It. (B) Data set life expectancy developing, 1407 Tr. et 20 It.
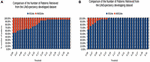
Figure 6. Exp. 1 Data set life expectancy developing. (A) Exp. 1 data set life expectancy developed. (B) Exp. 1 data set life expectancy developing.
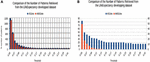
Figure 7. Exp. 2 Data set life expectancy. (A) Exp. 2 data set life expectancy developed. (B) Exp. 2 data set life expectancy developing.
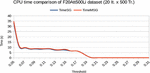
Figure 8. Different CPU times [Tr. (Resp. It.) denotes transactions (resp. Items)] forF20Att500Li 500 Tr. et 20 It.

Figure 9. Experimentation of data set F20Att500Li on number gradual patterns extracted. (A) Exp. 1 data set F20Att500Li. (B) Exp. 2 data set F20Att500Li.
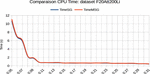
Figure 10. Different CPU times [Tr. (Resp. It.) denotes transactions (resp. Items)] forF20Att200Li 200 Tr. et 20 It.

Figure 11. Experimentation of data set F20Att200Li on number gradual patterns extracted. (A) Exp. 1 data set F20Att200Li. (B) Exp. 2 data set F20Att200Li.

Figure 12. Different CPU times [Tr. (Resp. It.) denotes transactions (resp. Items)] forF30Att100Li 100 Tr. et 30 It.
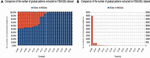
Figure 13. Experimentation of data set F30Att100Li on number gradual patterns extracted. (A) Exp. 1 data set F30Att100Li. (B) Exp. 2 data set F30Att100Li.
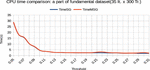
Figure 14. Different CPU times [Tr. (Resp. It.) denotes transactions (resp. Items)] data set fundamental, 300 Tr. et 35 It.
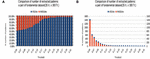
Figure 15. Experimentation of data set fundamental on number gradual patterns extracted. (A) Exp. 1 data set fundamental. (B) Exp. 2 data set fundamental.
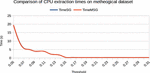
Figure 16. Comparison of execution times on meteorological data made up of 516 trans-actions and 26 items.

Figure 17. Experimentation of data set meteorological on number gradual patterns extracted. (A) Exp. 1 data set meteorological. (B) Exp. 2 data set meteorological.
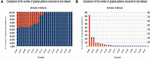
Figure 19. Experimentation of data set test on number gradual patterns extracted. (A) Exp. 1 data set test. (B) Exp. 2 data set test.
Conclusion
In this research, we describe a method for improving the efficiency of algorithms for detecting frequent and maximum gradual patterns by halving both the search space and the burden of the calculation of gradual supports on big datasets. Experiments on many types of well-known datasets indicate the efficacy of the suggested technique. In the future study, we will analyze larger datasets and investigate the possibility of distributed processing.
Footnotes
- ^ OnLine Transactional Processing.
References
1. Oudni A. Fouille de donnees par extraction de motifs graduels: contextualisation et enrichissement. Ph.D. thesis. Paris: Universite Pierre et Marie Curie (2014).
3. Ayouni S. Etude et extraction de regles graduelles floues: definition d’algorithmes efficaces. Ph.D. thesis. Montpellier: Universite Montpellier (2012).
4. Negrevergne B, Termier A, Rousset M, Mehaut J. Para miner: a generic pattern mining algorithm for multi-core architectures. Data Min Knowl Discov. (2014) 28:593–633. doi: 10.1007/s10618-013-0313-2
5. Clementin TD, Cabrel TFL, Belise KE. A novel algorithm for extracting frequent gradual patterns. Mach Learn Appl. (2021) 5:100068. doi: 10.1016/j.mlwa.2021.100068
6. Ngo T, Georgescu V, Laurent A, Libourel T, Mercier G. Mining spatial gradual patterns: Application to measurement of potentially avoidable hospitalizations. In: Tjoa AM, Bellatreche L, Biffl S, van Leeuwen J, Wiedermann J editors. SOFSEM 2018: Theory and practice of computer science, volume 10706. Cham: Springer International Publishing (2018). p. 596–608. doi: 10.1007/978-3-319-73117-9_42
7. Owuor D, Laurent A, Orero J. Mining fuzzy-temporal gradual patterns. In: Proceeding of the 2019 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE). New Orleans, LA: IEEE (2019). p. 1–6. doi: 10.1109/FUZZIEEE.2019.8858883
8. Shah F, Castelltort A, Laurent A. Handling missing values for mining gradual patterns from NoSQL graph databases. Future Gene Comput Syst. (2020) 111:523–38. doi: 10.1016/j.future.2019.10.004
9. Di Jorio L. Recherche de motifs graduels et application aux donnees medicales. Ph.D. thesis. Montpellier: University of Montpellier (2010).
10. Laurent A, Lesot M-J, Rifqi M. Extraction de motifs graduels par correlations d’ordres induits. In: Rencontres sur la Logique Floue et ses Applications, LFA’2010. Lannion (2010).
11. Di-Jorio L, Laurent A, Teisseire M. Mining frequent gradual item sets from large databases. In: Proceeding of the International Symposium on Intelligent Data Analysis. Berlin: Springer (2009). p. 297–308. doi: 10.1007/978-3-642-03915-7_26
12. Hullermeier E. Association rules for expressing gradual dependencies. In: Elomaa T, Mannila H, Toivonen H editors. Principles of data mining and knowledge discovery, PKDD lecture notes in computer science. Berlin: Springer (2002). p. 200–11. doi: 10.1007/3-540-45681-3_17
13. Berzal F, Cubero JC, Sanchez D, Miranda MAV, Serrano J. An alternative approach to discover gradual dependencies. Int J Uncertain Fuzziness Knowl Based Syst. (2007) 15:559–70. doi: 10.1142/S021848850700487X
14. Marsala C, Laurent A, Lesot M-J, Rifqi M, Castelltort A. Discovering ordinal attributes through gradual patterns, morphological filters and rank discrimination measures. In: Ciucci D, Pasi G, Vantaggi B editors. Scalable uncertainty management, lecture notes in computer science. Cham: Springer International Publishing (2018). p. 152–63. doi: 10.1007/978-3-030-00461-3_11
15. Aryadinata YS, Lin Y, Barcellos C, Laurent A, Libourel T. Mining epidemiological dengue fever data from Brazil: a gradual pattern based geographical information system. In: Laurent A, Strauss O, Bouchon-Meunier B, Yager RR editors. Information processing and management of uncertainty in knowledge-based systems, communications in computer and information science. Cham: Springer International Publishing (2014). p. 414–23. doi: 10.1007/978-3-319-08855-6_42