Introduction
Transcranial stimulation is a technique to excite the brain using electromagnetic induction: a changing magnetic field induces an electric field that activates the neurons. The main advantage of magnetic stimulation over electrical stimulation is that it is non-invasive and painless. Magnetic stimulation has a long history (1). This review focuses on developments that occurred in the 1980s and 1990s, when magnetic stimulation was introduced as a research and clinical tool. Although I survey the entire body of research, the emphasis is on work done at the National Institutes of Health (NIH). The goal of this review is to introduce the history and principles of magnetic stimulation to young investigators and researchers not familiar with the topic.
Effects of coil design on delivery of focal magnetic stimulation
I joined the Biomedical Engineering and Instrumentation Program at the NIH in the fall of 1988. The NIH intramural program is located on a large campus in Bethesda, Maryland, just outside of Washington, DC Most of the NIH researchers at that time were focused on biochemistry and genetics, but there were so many scientists at the NIH campus that, nevertheless, many were interested in neurophysiology. The goal of the Biomedical Engineering and Instrumentation Program, then led by Murray Eden, was to have its physicists, engineers, and mathematicians collaborate with biologists and medical doctors working in the disease institutes. I arrived soon after receiving my PhD in physics from Vanderbilt University, where I had measured the magnetic field produced by nerves and muscle.
One of my first tasks at NIH was to meet with two medical doctors in the National Institute of Neurological Disorders and Stroke—Mark Hallett and Leo Cohen—who had recently begun using magnetic stimulation. Hallett obtained his medical degree from Harvard and was chief of the Human Motor Control Section, housed in NIH’s famous clinical center. He is a leading figure in neurophysiology, specifically in magnetic stimulation research, and is often asked to publish tutorials about magnetic stimulation in leading journals (2, 3). Hallett once told me that he began college as a physics major but switched to a pre-med program after a year or 2. Cohen earned his MD from the University of Buenos Aires in Argentina. In the late 1980s, he worked in Hallett’s section, but eventually became the head of his own Human Cortical Physiology Section at NIH. Together Hallett and Cohen were doing ground-breaking research in magnetic stimulation but lacked the technical expertise in physics required to do things like calculate the electric fields produced by different coils.
At that time, magnetic stimulation was only a few years old. It was invented by Tony Barker, an English clinical engineer at the Royal Hallamshire Hospital in Sheffield, who obtained his PhD from the University of Sheffield. His landmark invention would eventually earn him awards, including the International Brain Stimulation Award in 2017. Working with his student Mike Polson and collaborator Ian Freeston, Barker developed a method to stimulate peripheral nerves in the arm using a time-varying magnetic field (4). Subsequently, Barker, Freeston, and another student, Reza Jalinous, built a more powerful device to stimulate the brain. In a recent interview with neurophysiologist John Rothwell.1 Barker described how he travelled to the Institute of Neurology at Queen Square in London to demonstrate his stimulator to the prominent neurophysiologist Pat Merton. Merton had developed an electrical method to stimulate the brain, but it was painful because in order to produce a sufficient electric field in the brain to excite neurons, a much larger electric field was created in the scalp (5). In magnetic stimulation, on the other hand, the magnetic field passed through the skull and induced an electric field in the brain that was similar in magnitude to that produced in the scalp, so it was virtually painless. Barker’s visit caused a stir among neurophysiologists at Queen Square and triggered an avalanche of research on magnetic stimulation. Following the meeting, Barker published a two-page paper in the leading British medical journal The Lancet. This publication marks the birth of modern transcranial magnetic stimulation. It has been cited over 5,000 times in the scientific literature (6).
Over the next few years, Barker and his team continued to develop magnetic stimulation (7–10). A group at Queen Square that included Christian Hess, Kerry Mills, and Nick Murray found that magnetic stimulation of the brain could elicit contractions of small muscles in the hand, such as the abductor digiti minimi, and they could measure conduction times for propagation in the central and peripheral nervous systems (11–13). Another group at Queen Square, including John Rothwell and Brian Day and led by the eminent neurophysiologist C. David Marsden, explored if electric and magnetic stimulation activated different neuronal elements in the brain (14, 15). Although these studies all made use of a circular coil, Shoogo Ueno and his coworkers, working at Kyushu University in Fukuoka, Japan, found that two side-by-side circular coils, forming a figure-8 shape, resulted in a stronger, more localized stimulus (16, 17). The figure-8 coil soon became the most widely used coil design for magnetic stimulation. The field of magnetic stimulation through 1987 was summarized in the book Magnetic Stimulation in Clinical Neurophysiology, edited by Sudhansu Chokroverty.
Hallett and Cohen obtained a magnetic stimulator at NIH in the late 1980s. They described magnetic stimulation and its potential uses in the Journal of the American Medical Association (18), where they highlighted how assessment of central conduction times using magnetic stimulation could be useful for diagnosing diseases, such as multiple sclerosis, and also how the method could be suitable for monitoring the integrity of the spinal cord during surgery. They emphasized that although methods existed to measure the conduction time in the brain for sensory fibers, stimulation of the brain was needed to measure conduction times in central motor fibers.
Not entirely realizing the explosion of research I was lucky enough to be wading into, I started collaborating with Hallett and Cohen to calculate the electric fields produced during magnetic stimulation (the details of those calculations are described in the next section). Our first work together was a technical paper comparing the electric and magnetic fields produced by a variety of coils with different shapes (19). The electric field under a round coil was largest under the coil perimeter and was zero below its center (Figure 1). The stimulator produced a magnetic field of 1–2 T by passing a current of several kiloamps through the coil in a pulse lasting for approximately one-tenth of the millisecond. The resulting peak electric field 1 cm below the coil was about 400 V/m, which was more than sufficient for neural excitation. The field was even stronger and more localized under a figure-8 coil (Figure 2).

Figure 1. The magnitude of the electric field (red) in a plane 1 cm below a circular coil. The coil (purple) had a diameter of 5 cm, 14 turns, and carried a current changing at a rate of 150 kA/ms. Adapted from Figure 5C of Cohen et al. (19).

Figure 2. The magnitude of the electric field (red) in a plane 1 cm below a figure-8 coil. The coil (purple) had 15 turns and carried a current changing at a rate of 150 kA/ms. Adapted from Figure 5F of Cohen et al. (19).
The electric field induced during magnetic stimulation
In August 1989, I attended the International Motor Evoked Potential Symposium in Chicago, Illinois, where I met many of the leaders in magnetic stimulation research. Papers associated with talks at that meeting were published in the journal Electroencephalography and Clinical Neurophysiology (Supplement 43, 1991). In a paper with Cohen and Hallett, I described the mathematical method I used to calculate the electric field produced by a coil (20).
I approximated the coil as a polygon. The advantage of a polygon is that I could derive an analytical solution for the electric field produced by a straight wire and then I could add the contributions of all the line segments to obtain the electric field of the entire coil. The equation for the electric field was as follows:
where μo was a constant (4π 10–7 T m/A), N was the number of turns, dI/dt was the rate of change of the coil current, r was the position where the electric field was calculated, and r′ was the location of the segment of coil dl′. The details of how to evaluate this integral for a straight segment of coil were given in the appendix of Roth et al. (20). The final result was given as follows:
where sinh−1 was the inverse hyperbolic sine function, δ was a vector equal to the difference between the two end points of the line segment, R was the vector from the midpoint of the line segment to r, ϕ was the angle between R and δ, and R and δ were the lengths of R and δ. The inverse hyperbolic sine function can be written in terms of the natural logarithm, so an alternative expression for the electric field is given as follows:
The only part of the integral that varies with time is the coil current, so the expression for the electric field separates into the product of dI(t)/dt and a time-independent expression that depends on the coil geometry. The integral in Equation (1) is dimensionless (dl′ has units of length, and so does r – r′). This implies that the electric field one coil radius below a 10-cm circular coil is the same as the electric field one coil radius below a 1-cm circular coil. The length scale (or, in other words, the unit for length) is irrelevant. The logarithm function changes notoriously slowly; if the argument inside the bracket in Equation (3) is 1000, its natural logarithm is less than 7. Therefore, in terms of an order of magnitude, the electric field produced by the coil is 0.1 N dI(t), where the electric field has units of volts per meter (V/m) and the rate of change of the current has units of kiloamps per millisecond (kA/ms).
Although these expressions were useful, they did not tell the entire story. They gave the electric field caused directly by electromagnetic induction. However, an electric field could also be produced by charge accumulating at the tissue surface. For example, suppose you held a magnetic coil perpendicular to the surface of the body.
The electric field due to induction would be directed in circular loops concentric with the coil (Figure 3A). This electric field would cause current to flow in the tissue. However, that current could not flow into the surrounding air, an insulator, so charge would accumulate at the tissue surface (shown by the green plus and minus signs) until the perpendicular component of the electric field produced by the charge (Figure 3B) was equal and opposite to the perpendicular component of the electric field produced by induction. This effect happened not only at the air–tissue interface but also at any boundary between regions of different electrical conductivity. You could determine the electric field that charge produced by solving Laplace’s equation for the voltage (20, 21).
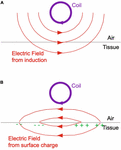
Figure 3. (A,B) A schematic drawing of the electric field (red) produced by electromagnetic induction (top) and surface charge (bottom). The coil (purple) was oriented perpendicular to the tissue surface. Adapted from Figure 1 of Roth et al. (20).
For example, suppose you viewed the circular coil of Figure 3 from above (Figure 4). The total electric field (from both induction and charge) is restricted to planes parallel to the tissue surface. It is strongest directly below the coil and spreads out in loops on both sides of the coil. Moreover, the peak electric field is weaker than if no tissue had been present. The electric field from charge partially cancels the inductive electric field, making stimulation more difficult.

Figure 4. The electric field (red lines) produced by a circular coil held perpendicular to a tissue having a flat surface. The coil (purple), seen edge on from above, had a diameter of 5 cm, 10 turns, and carried a current changing at a rate of 100 kA/ms. The nearest edge of the coil was 0.5 cm above the tissue surface, and the electric field was calculated 1 cm below the surface. Adapted from Figure 2 of Roth et al. (20).
My initial interest was in magnetic stimulation of peripheral nerves, despite such stimulation being not as suitable for routine nerve conduction studies as it was for brain studies (22). So, my first calculation that included the effect of the tissue boundary was of the electric field induced in a cylindrical arm (21). Figure 5 shows the distribution of the electric field in the arm when a coil is held near it. The field is largest at the top of the arm under the edge of the coil, but it is also large and in the opposite direction on the right surface of the arm below the center of the coil.

Figure 5. A contour map of the axial component (into the paper in the end view) of the electric field in a cylindrical arm when a 5 cm diameter, 10 turn coil (purple) carrying a current increasing at a rate of 100 kA/ms was placed 1 cm over the arm edge. The electric field values (red) are given in V/m. Adapted from Figure 7 in Roth et al. (21).
I was not the only researcher calculating electric fields produced during magnetic stimulation. Paul Tofts, a physicist at Queen Square, performed similar calculations, including dividing the electric field into two parts, one caused by induction and the other by charge, although his calculations were only for circular coils as opposed to my computations for any coil geometry using my line segment approximation (23, 24). He also carried out experiments to measure the electric field using a bipolar probe in a saline bath below the coil. Following his research into magnetic stimulation, Tofts became known for his work developing dynamic contrast-enhanced magnetic resonance imaging. Dominique Durand and his collaborators in the Department of Biomedical Engineering at Case Western Reserve University further examined the effect of charge accumulation on the tissue surface (25); Ferdinando Grandori and Paolo Ravazzani, at the Polytechnic University of Milan in Italy, examined coils with different sizes and orientations (26); Kent Davey and his collaborators performed similar calculations at the Georgia Institute of Technology (27); and J. Patrick Reilly of the Johns Hopkins Applied Physics Laboratory calculated electric fields in the body produced by a changing magnetic field, although primarily in the context of neural stimulation caused by magnetic resonance imaging (MRI) (28, 29). The field was becoming quite crowded.
A theoretical calculation of the electric field induced in the cortex during magnetic stimulation
Hallett and Cohen were most interested in the electric field induced during transcranial magnetic stimulation, so my next task was to use a three-sphere model to calculate the electric field in the brain (30). I had help from an undergraduate engineering student from Brown University, Joshua Saypol, who worked at NIH during his summer breaks. Saypol and I represented the head as three concentric spherical layers: the scalp, skull, and brain. We were able to calculate the electric field just below the brain surface using the method described in the last section. Saypol then compared the electric field induced during transcranial magnetic stimulation to that produced by electrical stimulation using electrodes on the scalp (31, 32). He found that transcranial magnetic stimulation using a figure-8 coil created a more localized stimulus than did electrical stimulation with two closely spaced scalp electrodes (Figure 6). The main reason for the superior focality during magnetic stimulation was that the high-resistance skull not only reduced the fraction of the current reaching the brain during electric stimulation, but also spread out the spatial distribution of that current within the brain. One often-cited disadvantage of magnetic stimulation is the lack of spatial resolution, and that is true when compared to electrical stimulation of the exposed cortex, but compared to using scalp electrodes, the spatial resolution of magnetic stimulation is impressive.

Figure 6. A contour map of the magnitude of the electric field (red) 0.3 cm below the surface of the brain, produced by magnetic stimulation with a figure-8 coil (purple) and by electric stimulation using closely spaced electrodes on the scalp (green). The head was represented using a three-sphere model (brain, skull, and scalp). During magnetic stimulation, the figure-8 coil had 15 turns, was 1 cm above the top of the head, and carried a current changing at a rate of 25 kA/ms. During electric stimulation, the electrodes passed a current of 566 mA. The electric field strength was given in V/m. Adapted from Figure 1 of Saypol et al. (31).
Again, other researchers were also analyzing brain stimulation. Harry Eaton, an engineer at the Johns Hopkins Applied Physics Lab, derived a detailed analytical model of transcranial magnetic stimulation that even included the capacitive properties of the tissue, a factor I had ignored (33). Leon Heller and David van Hulsteyn from Los Alamos National Laboratory analyzed brain stimulation and showed that the radial electric field in the brain vanished (34), a point independently made by David Cohen and B. Neil Cuffin from the Massachusetts Institute of Technology (35). Saypol and I had found that the radial component of the electric field in the brain was very small, but now we realized that we were just looking at the numerical error in our solution to Laplace’s equation, and a more accurate calculation would give zero radial field (31). This result was quite different than for electrical stimulation using scalp electrodes, where the electric field was primarily radial. Heller and van Hulsteyn also proved that the electric field deep in the brain can never be larger than the electric field at its surface, regardless of the coil design (assuming a homogeneous tissue). No clever coil shape can create “hot spots” of strong electric field deep in the brain.
Nowadays the electric field in the brain can be calculated using more powerful finite element methods. For instance, Pedro Miranda, a physicist from the University of Lisbon, and his colleagues calculated the electric field produced during transcranial magnetic stimulation (36). Their calculation included heterogeneity and anisotropy, which can significantly affect the electric field distribution. Tim Wagner of MIT and his coworkers performed a finite element calculation that included a realistic shape for the brain and found that modifications to the cortical geometry could perturb the predicted site of excitation (37).
The research at NIH was assisted by an outstanding group of young scientists who worked with Hallett and Cohen. For example, the Brazilian neurologist Joaquim Brasil-Neto examined how the orientation of the electric field influenced the stimulation threshold (38). I was a co-author on this paper because I contributed a few electric field calculations, and it is now my most highly cited publication. Peter Fuhr analyzed how the latency of motor-evoked potentials depended on the position of the stimulating coil relative to the head (39). The NIH group used magnetic stimulation to create topographic maps of the brain in patients with amputations, spinal cord injuries, and mirror movement disorders (40). Much of this research was described in an article published in a special issue of the Journal of Clinical Neurophysiology dedicated to magnetic stimulation (41).
A model of the stimulation of a nerve fiber by electromagnetic induction
Determining the electric field distribution produced by a coil was important, but equally important was analyzing how that electric field coupled to a nerve. Frank Rattay had previously derived an “activating function” for electrical stimulation of a long peripheral nerve (42). Polarization of an axon occurs where the second derivative of the voltage along the axon is largest. A similar activating function exists for magnetic stimulation. However, you cannot describe an electric field caused by electromagnetic induction in terms of a voltage. Instead, you need to express the activating function in terms of the electric field itself. I derived such an activating function for magnetic stimulation in collaboration with Peter Basser.
Basser obtained his PhD in engineering from Harvard and joined the Biomedical Engineering and Instrumentation Program just a year or 2 before I did. Together, we determined that polarization occurs along the axon where the gradient of the electric field is largest (21). If you are reading that paper, be aware that we published two errata (43, 44). In addition to his work on magnetic stimulation (45, 46), Basser is famous for developing MRI diffusion tensor imaging and was awarded a gold medal from the International Society of Magnetic Resonance in Medicine.
Our analysis was based on a rederivation of the nerve cable equation, including a term containing the electric field produced by the coil,
where λ and τ were the axon length and time constants, respectively, V was the transmembrane potential, x was the position along the axon, and Ex was the component of the stimulating electric field parallel to the axon during magnetic stimulation. The term on the right-hand side of the equation was called the activating function, following Rattay’s nomenclature. It acted as the source term for the transmembrane potential. Depolarization and excitation should occur where dEx/dx is negative in sign and large in magnitude. In retrospect, this result seems obvious given Rattay’s analogous activating function for electrical stimulation, but at the time, it was quite a surprise.
As an example, we considered a peripheral nerve being stimulated by magnetic stimulation (Figure 7). The nerve (light blue) was long and straight and passed 1 cm below the edge of a circular coil (purple). Along the nerve, the electric field pointed in the negative x direction and was largest just below the coil. However, this was not where the nerve would be depolarized (meaning its transmembrane potential was raised toward the threshold for excitation). Instead, the nerve would be depolarized 2 or 3 cm away, where the gradient of the electric field was largest. It would also be hyperpolarized (its transmembrane potential was lowered below rest, opposing excitation) 2 or 3 cm along the nerve in the other direction. If you changed the polarity of the stimulus, the location of depolarization and hyperpolarization would switch, resulting in a testable prediction: Measure the arrival time of the action potential at the far end of the nerve for one polarity of the stimulus and then for the other (easily done by flipping the coil over). There should be a latency difference between the two arrival times because in one case the nerve must propagate about 4 or 5 cm farther than in the other.

Figure 7. A contour plot of dEx /dx (green), 1 cm below the plane of a circular coil, where x was the direction parallel to the nerve (light blue) and Ex was the component of the electric field along the nerve. The coil (purple) had 30 turns, a diameter of 5 cm, and carried a current changing at a rate of 1 kA/ms. Adapted from Figure 3 of Roth and Basser (21).
Basser and I took the calculation further. We implemented the Hodgkin and Huxley model describing the ion channels in the axon membrane, calculated where and when stimulation occurred, and predicted all the propagation dynamics (47). We even modified the model to include a myelinated axon in a cylindrical arm, so we could make more accurate predictions (48).
Again, other researchers were developing similar models. Durand, with his student Sri Nagarajan, analyzed where excitation occurred along a nerve fiber (49, 50). They found results similar to ours, but also found that when the nerve is not long, excitation can occur at its end. This mechanism operates where the electric field itself is large, not where its gradient is large. Maria Stuchly and her team in Canada made additional contributions (51, 52).
Determining the site of stimulation during magnetic stimulation of a peripheral nerve
I was anxious to test the prediction of where excitation occurs along a peripheral nerve during magnetic stimulation. The ideal experiment would be to dissect a nerve, place it in a dish filled with saline, and then stimulate it. However, Hallett and Cohen were focused mainly on clinical applications, so we tested the prediction in humans (53). The experiment was performed by Marcela Panizza, an Italian medical doctor, and her husband Jan Nilsson, a biomedical engineer originally from Denmark but working with Panizza in Italy. Panizza and Nilsson would often visit NIH to collaborate with Hallett and Cohen. In the experiment, the median nerve was stimulated at the forearm and the motor response was recorded using electrodes attached to the thumb. Figure 8 shows a latency shift in the motor response of about 0.65 ms obtained upon switching the polarity of the stimulus by flipping the coil over. The propagation velocity was about 60 m/s, implying a shift in the position of excitation of nearly 4 cm, close to that predicted by our calculations. Nilsson and Panizza also used electrical stimulation to create a map of how propagation time related to position along the arm and then used this calibration curve to show that magnetic stimulation did not occur where the electric field was largest, but instead where its spatial derivative was largest.
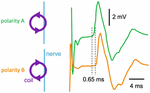
Figure 8. Motor fiber compound action potential for two polarities of magnetic stimulation, recorded at the distal end of the human median nerve during stimulation with a circular coil. Adapted from Figure 6A in Nilsson et al. (53).
Although this experiment confirmed our prediction, there were nevertheless concerns because of the heterogeneous nature of the bones and muscles in the human arm. At about the same time Nilsson and Panizza were doing their experiment at NIH, Paul Maccabee was performing an even better experiment at the New York Down state Medical Center in Brooklyn. Maccabee obtained his MD from Boston University and collaborated in Brooklyn with the internationally acclaimed neuroscientist Vahe Ammasian (55–59). This research culminated in their 1,993 article in the Journal of Physiology, in which they examined magnetic stimulation of a peripheral nerve lying in a saline bath (54). First, they measured the electric field Ey (they assumed the nerve would lie above the coil along the y-axis) and its derivative along the nerve produced by a figure-8 coil located under the bath (Figure 9). They found that the electric field was maximum directly under the center of the coil, but the magnitude of the gradient dEy/dy was maximum a couple centimeters either side of the center.

Figure 9. Contour plots of the electric field (Ey, red) and its spatial derivative (dEy /dy, blue) induced by a figure-eight coil (purple) placed under a tank filled with saline and measured using a bipolar recording electrode. The y direction is downward in the figure, parallel to the direction of the nerve (see Figure 10). Adapted from Figure 2 of Maccabee et al. (54).
Next they placed a bullfrog sciatic nerve in the dish and recorded the electrical response from one end (Figure 10). They found a 0.9 ms delay between the recorded action potentials when the polarity of a magnetic stimulus was reversed (the yellow and red traces on the right). Given a propagation speed of about 40 m/s, the shift in excitation position was about 3.6 cm, consistent with what Basser and I would predict.

Figure 10. Recordings from an electrode (black dot) at the distal end of a bullfrog sciatic nerve (green) that was immersed in a trough filled with saline (blue) and stimulated with a figure-8 coil (purple). The nerve emerged from the saline to rest on the recording electrode in air. The compound nerve action potentials were elicited by a stimulus of one polarity (orange), then the other (red). Adapted from Figure 3 of Maccabee et al. (54).
So far, their study was similar to what we performed at NIH in a human, but then they did an experiment that we could not do. To determine how a heterogeneity would impact their results, they placed two insulating cylinders on either side of the nerve (Figure 11). These cylinders modified the electric field, moving the negative and positive peaks of the activating function closer together. They observed a corresponding reduction in the latency shift. This experiment provided insight into what happens when a human nerve passes between two bones, or some similar heterogeneity.

Figure 11. Magnetic stimulation of a sheep phrenic nerve immersed in a homogeneous (left) and inhomogeneous (right) volume conductor. The figure-8 coil (purple) was positioned under the nerve (green). The yellow circles indicate the position of the insulating cylinders. The electric field Ex (red) and its gradient dEx/dx (blue) were measured along the nerve trajectory. The compound nerve action potentials at the recording electrode were measured for a magnetic stimulus of one polarity (orange) and then the other (green). Adapted from Figure 5 of Maccabee et al. (54).
Finally, they changed the experiment by bending the nerve and found that a bend caused a low threshold “hot spot,” and that excitation at that spot occurred where the electric field, not its gradient, was large. This result was consistent with Nagarajan and Durand’s analysis of excitation of truncated nerves (49).
In my opinion, Maccabee’s (54) article is the most impressive publication in the magnetic stimulation literature. Only Barker’s original demonstration of transcranial magnetic stimulation can compete with it (6).
Just when it seemed the prediction was established that dEx/dx determined the location of excitation, Jarmo Ruohonen, working with coworkers in Italy, including Panizza and Nilsson, challenged this conclusion (60). They presented data indicating that the transverse component of the electric field, rather than the component parallel to the axon length, could cause excitation. According to the activating function idea, if a nerve passed directly below the center of a circular coil, no excitation should occur because the gradient of the electric field, and indeed the electric field parallel to the direction of the nerve, was zero. However, Ruohonen and his collaborators found that sometimes excitation did occur in this configuration. The result was difficult to explain, because a transverse field ought to depolarize one side of an axon and hyperpolarize the other, so their effects cancel out. Moreover, because the axon radius is so small (typically tens of microns), the threshold for excitation by a transverse field should be very high. Viet Schnabel and Johannes Struijk, working at Aalborg University in Denmark, examined this issue. They found that transverse stimulation may occur because the axons in a nerve undulate (61). The model Basser and I derived assumed that the axon was straight, although we did note that if the axon followed a sinuous path the activating function would have to be evaluated along it (47). Schnabel and Struijk concluded that even a small amount of undulation (say, 20 μm) could trigger excitation by a transverse field. It is an important reminder that we must always be aware of the assumptions underlying a mathematical model.
In vitro evaluation of a four-leaf coil design for magnetic stimulation of peripheral nerve
One frustrating feature of the activating function approach is that excitation does not occur directly under the center of a figure-8 coil, where the electric field is largest, but off to one side, where the gradient peaks (Figure 9). Medical doctors do not want to guess how far from the coil center excitation occurs; they would prefer a coil for which “x” marks the spot. It occurred to me that such a coil could be designed using two adjacent figure-8 coils. I called this the four-leaf coil (Figure 12). John Cadwell from Cadwell Laboratories (Kennewick, Washington, DC, USA) built such a coil for me. Having seen the excellent results that Maccabee was obtaining using his nerve-in-a-dish setup, I sent the coil to him so he could test it. The resulting paper (62) showed that for one polarity of the stimulus the magnitude of the gradient of the electric field was largest directly under the coil center so the axons there were depolarized (“x” really did mark the spot of excitation). In addition, if the polarity of the stimulus was reversed, the magnitude of the gradient remained large under the coil center, but it now tended to hyperpolarize rather than depolarize the axons. Maccabee and I hoped that such hyperpolarization could be used to block action potential propagation, acting like an anesthetic. The Brooklyn experiments verified all the predictions of the activating function model for the four-leaf coil. Unfortunately, Maccabee never observed any action potential block. Perhaps, the hyperpolarization required for block was greater than the coil could produce.

Figure 12. A four-leaf coil (purple) used to stimulate a peripheral nerve (blue). Adapted from Figure 1 of Roth et al. (62).
The four-leaf coil is not widely used in transcranial magnetic stimulation. It is based on the assumption that you are stimulating a long, straight peripheral nerve, so dEx/dx is the relevant quantity to determine excitation. In the brain, where bending, truncating axons are common, the electric field itself is probably the relevant quantity, not its gradient, so a figure-8 coil is superior to a four-leaf coil. Researchers who use the dEx/dx concept for brain stimulation are making a mistake.
Coil design has been an important part of magnetic stimulation research (Figure 13). Yiftach Roth (no relation) proposed the “H-coil,” which was designed to excite deep brain structures (63, 64). With Shokrollah Momen and Robert Turner, I used an inverse problem technique to predict a new design for a figure-8 coil in which the various turns of the coil were all tightly packed under the coil center, but splayed out in a variety of sized loops on its periphery (65). Chunye Ren and his collaborators at the University of Miami designed a coil shaped like a slinky (66). Karl Kraus and his collaborators developed a “cap coil” that was optimized for spinal cord monitoring (67). Eugen Lontis and his coworkers in Denmark designed a “cone coil” with improved focality (68). Ruohonen and his coworkers proposed a multichannel system consisting of an array of many small coils (69). The current could be independently varied in each coil to produce almost any electric field distribution the user desired. Coil design continues to be an active area of study to this day (70).

Figure 13. Different coil designs. Clockwise from top left: A slinky coil, a coil based on an inverse calculation, a cap coil, and a cone coil.
David Cohen attempted to make a very small magnetic stimulation coil in order to improve the spatial resolution of the stimulus (35). He found that as the coil became smaller, he had to use more and more current until the magnetic forces between different parts of the coil winding tore the coil apart. Even if he had been successful, the spatial resolution was limited as much by the distance from the coil to the brain, set by the thickness of the scalp and skull, as by the radius of the coil itself. Lee et al. (71) have claimed they can perform magnetic stimulation using an implanted microcoil having one turn with a diameter of about 100 μm and carrying a current of about 50 mA. They calculated the electric field produced by such a coil, but their results were far larger than what I would predict using Equation (2). I have not been able to reproduce their calculations, and they may in fact be observing capacitive coupling rather than magnetic stimulation (for more, see).2
Relevance of stimulus duration for activation of motor and sensory fibers
So far, we have considered the spatial distribution of the electric field, but we have not analyzed how it changes with time. A typical magnetic stimulator produces a brief stimulus pulse, about one-tenth of a millisecond in duration, by discharging a capacitor through the coil. A simplified stimulator circuit is shown in Figure 14 (72). Initially, the switch is to the left and the capacitor C is charged by the power supply. When ready to stimulate, the switch is thrown to the right and the charge stored in the capacitor is discharged through the coil, represented by in the circuit by its resistance R and inductance L.

Figure 14. A simplified circuit diagram for a magnetic stimulator, containing a power supply (blue), a switch (orange), a capacitor (green), and a coil represented by its resistance (red) and inductance (purple).
When the switch is thrown, the current I in the coil cannot turn on instantaneously because of the coil inductance. Instead, it rises to a maximum and then falls. In a circuit containing a capacitor and inductor, the current will typically not decay to zero but instead will overshoot zero, reversing direction. Such oscillations will continue, but the coil resistance will cause their amplitude to ultimately decay (Figure 15, upper left). The electric field induced in the brain varies as the rate of change of the coil current, dI/dt. The rate of change turns on abruptly and then oscillates out of phase with the coil current (Figure 15, upper right). Some stimulators include a diode in the circuit (a diode can only pass current in one direction), suppressing oscillations (Figure 15, lower left). However, even in this case, dI/dt is not “monophasic” (entirely one polarity). The rate of change will be positive as the coil current rises to its peak and then negative as it decays. This rate of change is analogous to the current through an electrode during electrical stimulation. However, it always changes from positive to negative and is biphasic for a circuit with a diode (Figure 15, lower right). A truly monophasic stimulus pulse for magnetic stimulation is impossible.

Figure 15. The coil current (left) and its rate of change (right) through a coil during magnetic stimulation, for a circuit without a diode (top) and with a diode (bottom).
Stimulators without a diode, such as those manufactured by Cadwell Laboratories and used at NIH in the 1990s, could produce a powerful stimulus. They were often useful for clinical studies, but sometimes the oscillating stimulus could make it a confusing research tool. Stimulators with a diode, such as those manufactured by Dantec Electronics (Skovlunde, Denmark) and also used at NIH, provided a biphasic stimulus, but the first phase was brief and strong whereas the second phase was long and weak. The first phase acted as the main stimulus, being somewhat analogous to a monophasic electric stimulus.
Panizza and Nilsson performed experiments at NIH examining both electric and magnetic stimulation of peripheral motor and sensory nerves (73). Shorter duration stimuli selectively stimulate motor fibers, while longer duration stimuli selectively stimulate sensory fibers. The magnetic stimulation pulse acts like a brief stimulus, so the threshold for motor fibers is lower than for sensory fibers.
To better compare magnetic and electric stimuli, I modeled the electric stimulus as a square pulse and the magnetic stimulus as triangular: an instantaneous upstroke followed by a linear decay (ignoring the weaker second phase). I found that the strength–duration curves for these two cases were different (Figure 16). The rheobase (the threshold for a long stimulus) was the same in both cases, but the chronaxie (the threshold duration for a strength of twice rheobase) was more than three times longer for magnetic than electric stimulation.

Figure 16. A log–log plot of the strength–duration curve for electric (blue) and magnetic (red) stimulation. The electric curve was determined using a square stimulus pulse, and the magnetic curve was determined using a triangular stimulus pulse. The strength is in terms of multiples of the rheobase, and the duration is in terms of multiples of the axon time constant.
The heating of metal electrodes during rapid-rate magnetic stimulation: a possible safety hazard
Transcranial magnetic stimulation is a powerful research and clinical tool, but is it safe? Eric Wassermann—a medical doctor who trained with Hallett and was editor of the Oxford Handbook of Transcranial Stimulation—wrote a review of safety issues based on an international workshop held in June 1996 (74). This review was updated by Simone Rossi and his collaborators a decade later (75). Concerns about safety focus on rapid rate magnetic stimulation, when trains of stimuli are produced at rates as high as 60 stimuli per second. Seizures are one potential safety hazard but are rare. Magnetic stimulation produces a magnetic field of a few tesla, which can exert forces on magnetic objects. The magnetic stimulator could in theory interfere with implanted medical devices. Magnetic forces between turns in a coil can produce surprisingly loud, brief sounds. S. Allen Counter and his collaborators have found evidence of acoustic trauma arising from transcranial magnetic stimulation and recommend using ear plugs (76).
One of the most serious safety hazards was discovered by Alvaro Pascual-Leone, a Spanish MD/PhD who trained at NIH in the 1990s. Pascual-Leone and his colleagues wanted to record the electroencephalogram (EEG) during and immediately following rapid rate transcranial magnetic stimulation, so they stimulated with silver EEG recording electrodes placed over the scalp. One patient suffered a burn under an electrode (77). To examine if this was caused by Joule heating from the induced eddy currents in the electrode, Pascual-Leone and I measured the temperature of different electrodes with different sizes and made from different metals (44). During stimulation, the temperature rose and then returned to its original value in about a minute or 2 after stimulation ended (Figure 17). We were able to determine what total number of stimuli and what rate of stimulation were safe, and which were unsafe. Interestingly, we could reduce the increase in temperature dramatically by cutting a slot in the EEG electrode, which did not affect its ability to record the EEG but did reduce the eddy currents induced in the silver significantly. Pascual-Leone went on to become a professor of neurology at Harvard Medical School and received the Ramón y Cajal Award in Neuroscience. In 2002, he was the lead editor on the Handbook of Transcranial Magnetic Stimulation.

Figure 17. The temperature increase of a silver EEG electrode attached to the forearm, as a function of time. In each case the electrode received 40 magnetic stimulation pulses, but they were delivered at different frequencies. After the train of stimuli ended, the electrode cooled with a time constant of about 45 s. Adapted from Figure 3A of Roth et al. (78).
Conclusion
I summarized my work on magnetic stimulation in a review article in the CRC Critical Reviews of Biomedical Engineering (79) and then left the NIH and magnetic stimulation research in 1995. However, the field exploded as the 21st century began. Mark George, working at NIH, discovered that daily rapid rate transcranial magnetic stimulation affects mood and now the most common application of magnetic stimulation is in psychiatry (80). Brain stimulation has been approved by the Food and Drug Administration and applications are multiplying. Transcranial magnetic stimulation remains a vibrant and exciting field of research (81).
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Author contributions
The author wrote this review article alone and is, therefore, entirely accountable for its content.
Acknowledgments
This research would not have been possible without the contributions of many excellent collaborators, including MH, LC, PB, JS, and many others.
Footnotes
- ^ www.youtube.com/watch?v=1DI3EC2pQ44&t=645s
- ^ hobbieroth.blogspot.com/2016/12/implantable-microcoi ls-for.html
References
1. Geddes LA. History of magnetic stimulation of the nervous system. J Clin Neurophysiol. (1991) 8:3–9.
4. Polson MJ, Barker AT, Freeston IL. Stimulation of nerve trunks with time-varying magnetic fields. Med Biol Eng Comput. (1982) 20:243–4.
5. Merton PA, Morton HB. Stimulation of the cerebral cortex in the intact human subject. Nature. (1980) 285:227.
6. Barker AT, Jalinous R, Freeston IL. Non-invasive magnetic stimulation of human motor cortex. Lancet. (1985) 1:1106–7.
7. Barker AT, Freeston IL, Jalinous R, Jarratt JA. Clinical evaluation of conduction time measurements in central motor pathways using magnetic stimulation of the human brain. Lancet. (1986) 1:1325–6.
8. Barker AT, Freeston IL, Jalinous R, Jarratt JA. Magnetic stimulation of the human brain and peripheral nervous system: an introduction and the results of an initial clinical evaluation. Neurosurgery. (1987) 20:100–9.
9. Barker AT. An introduction to the basic principles of magnetic nerve stimulation. J Clin Neurophysiol. (1991) 8:26–37.
10. Barker AT, Garnham CW, Freeston IL. Magnetic nerve stimulation: the effect of waveform on efficiency, determination of neural membrane time constants and the measurement of stimulator output. Electroenceph Clin Neurophysiol Suppl. (1991) 43:227–37.
11. Hess CW, Mills KR, Murray NMF. Magnetic stimulation of the human brain: facilitation of motor responses by voluntary contraction of ipsilateral and contralateral muscles with additional observations on an amputee. Neurosci Lett. (1986) 71:235–40.
12. Hess CW, Mills KR, Murray NM, Schriefer TN. Magnetic brain stimulation: central motor conduction studies in multiple sclerosis. Ann Neurol. (1987) 22:744–52.
13. Hess CW, Mills KR, Murray NMF. Responses in small hand muscles from magnetic stimulation of the human brain. J Physiol. (1987) 388:397–419.
14. Day BL, Thompson PD, Dick JP, Nakashima K, Marsden CD. Different sites of action of electrical and magnetic stimulation of the human brain. Neurosci Lett. (1987) 75:101–6.
15. Day BL, Dressler D, Maertens de Noordhout A, Marsden CD, Nakashima K, Rothwell JC, et al. Electric and magnetic stimulation of human motor cortex: surface EMG and single motor unit responses. J Physiol. (1989) 412:449–73.
16. Ueno S, Tashiro T, Harada K. Localized stimulation of neural tissues in the brain by means of a paired configuration of time-varying magnetic fields. J Appl Phys. (1988) 64:5862–4.
18. Hallett M, Cohen LG. Magnetism: a new method for stimulation of nerve and brain. JAMA. (1989) 262:538–41.
19. Cohen LG, Roth BJ, Nilsson J, Dang N, Panizza M, Bandinelli S, et al. Effects of coil design on delivery of focal magnetic stimulation: technical considerations. Electroenceph Clin Neurophysiol. (1990) 75:350–7.
20. Roth BJ, Cohen LG, Hallett M. The electric field induced during magnetic stimulation. Electroenceph Clin Neurophysiol Suppl. (1991) 43:268–78.
21. Roth BJ, Basser PJ. A model of the stimulation of a nerve fiber by electromagnetic induction. IEEE Trans Biomed Eng. (1990) 37:588–97.
22. Evans BA, Litchy WJ, Daube JR. The utility of magnetic stimulation for routine peripheral nerve conduction studies. Muscle Nerve. (1988) 11:1074–8.
23. Branston NM, Tofts PS. Analysis of the distribution of currents induced by a changing magnetic field in a volume conductor. Phys Med Biol. (1991) 36:161–8.
24. Tofts PS. The distribution of induced currents in magnetic stimulation of the nervous system. Phys Med Biol. (1990) 35:1119–28.
25. Durand D, Ferguson AS, Dalbasti T. Effect of surface boundary on neuronal magnetic stimulation. IEEE Trans Biomed Eng. (1992) 39:58–64.
26. Grandori F, Ravazzani P. Magnetic stimulation of the motor cortex: theoretical considerations. IEEE Trans Biomed Eng. (1991) 38:180–91.
27. Davey KR, Cheng CH, Epstein CM. Prediction of magnetically induced electric fields in biological tissue. IEEE Trans Biomed Eng. (1991) 38:418–22.
28. Reilly JP. Peripheral nerve stimulation by induced electric currents: exposure to time-varying magnetic fields. Med Biol Eng Comput. (1989) 27:101–10.
29. Reilly JP. Magnetic field excitation of peripheral nerves and the heart: a comparison of thresholds. Med Biol Eng Comput. (1991) 29:571–9.
30. Roth BJ, Saypol JM, Hallett M, Cohen LG. A theoretical calculation of the electric field induced in the cortex during magnetic stimulation. Electroenceph Clin Neurophysiol. (1991) 81:47–56.
31. Saypol JM, Roth BJ, Cohen LG, Hallett M. A theoretical comparison of electric and magnetic stimulation of the brain. Ann Biomed Eng. (1991) 19:317–28.
32. Saypol JM, Roth BJ, Cohen LG, Hallett M. Erratum to “A theoretical comparison of electric and magnetic stimulation of the brain,” Ann Biomed Eng. (1992) 20:495.
33. Eaton H. Electric field induced in a spherical volume conductor from arbitrary coils: application to magnetic stimulation and MEG. Med Biol Eng Comput. (1992) 30:433–40.
34. Heller L, Hulsteyn DB. Brain stimulation using electromagnetic sources: theoretical aspects. Biophys J. (1992) 63:129–38.
35. Cohen D, Cuffin BN. Developing a more focal magnetic stimulator. Part I: some basic principles. J Clin Neurophysiol. (1991) 8:102–11.
36. Miranda PC, Hallett M, Basser PJ. The electric field induced in the brain by magnetic stimulation: a 3-D finite-element analysis of the effect of tissue heterogeneity and anisotropy. IEEE Trans Biomed Eng. (2003) 50:1074–85.
37. Wagner TA, Zahn M, Grodzinsky AJ, Pascual-Leone A. Three-dimensional head model simulation of transcranial magnetic stimulation. IEEE Trans Biomed Eng. (2004) 51:1586–98.
38. Brasil-Neto JP, Cohen LG, Panizza M, Nilsson J, Roth BJ, Hallett M. Optimal focal transcranial magnetic activation of the human motor cortex: effects of coil orientation, shape of the induced current pulse, and stimulus intensity. J Clin Neurophysiol. (1992) 9:132–6.
39. Fuhr P, Cohen LG, Roth BJ, Hallett M. Latency of motor evoked potentials to focal transcranial stimulation varies as a function of scalp positions stimulated. Electroenceph Clin Neurophsyiol. (1991) 81:81–9.
40. Cohen LG, Bandinelli S, Topka HR, Fuhr P, Roth BJ, Hallett M. Topographic maps of human motor cortex in normal and pathological conditions: mirror movements, amputations and spinal cord injuries. Electroenceph Clin Neurophysiol Suppl. (1991) 43:36–50.
41. Cohen LG, Roth BJ, Wassermann E, Topka H, Fuhr P, Schultz J, et al. Magnetic stimulation of the human cerebral cortex, an indicator of reorganization in motor pathways in certain pathological conditions. J Clin Neurophysiol. (1991) 8:56–65.
42. Rattay F. Modeling the excitation of fibers under surface electrodes. IEEE Trans Biomed Eng. (1988) 35:199–202.
43. Fayad ZA, Roth BJ, Basser PJ. Correction to “A model of the stimulation of a nerve fiber by electromagnetic stimulation.” IEEE Trans Biomed Eng. (1991) 38:1161–2.
44. Roth BJ, Basser PJ. Correction to “A model of the stimulation of a nerve fiber by electromagnetic induction.” IEEE Trans Biomed Eng. (1992) 39:1211.
46. Basser PJ, Wijesinghe RS, Roth BJ. The activating function for magnetic stimulation derived from a three-dimensional volume conductor model. IEEE Trans Biomed Eng. (1992) 39:1207–10.
47. Basser PJ, Roth BJ. Stimulation of a myelinated nerve axon by electromagnetic induction. Med Biol Eng Comput. (1991) 29:261–8.
48. Roth BJ, Cohen LG, Hallett M, Friauf W, Basser PJ. A theoretical calculation of the electric field induced by magnetic stimulation of a peripheral nerve. Muscle Nerve. (1990) 13:734–41.
49. Nagarajan SS, Durand DM, Warman EN. Effects of induced electric fields on finite neuronal structures: a simulation study. IEEE Trans Biomed Eng. (1993) 40:1175–88.
50. Nagarajan SS, Durand DM. A generalized cable equation for magnetic stimulation of axons. IEEE Trans Biomed Eng. (1996) 43:304–12.
51. Esselle KP, Stuchly MA. Neural stimulation with magnetic fields: Analysis of induced electric fields. IEEE Trans Biomed Eng. (1992) 39:693–700.
52. Stuchly MA, Esselle KP. Factors affecting neural stimulation with magnetic fields. Bioelectromagnetics Suppl. (1992) 13:191–204.
53. Nilsson J, Panizza M, Roth BJ, Basser PJ, Cohen LG, Caruso G, et al. Determining the site of stimulation during magnetic stimulation of a peripheral nerve. Electroenceph Clin Neurophysiol. (1992) 85:253–64.
54. Maccabee PJ, Amassian VE, Eberle LP, Cracco RQ. Magnetic coil stimulation of straight and bent amphibian and mammalian peripheral nerve in vitro: locus of excitation. J Physiol. (1993) 460:201–19.
55. Amassian VE, Eberle L, Maccabee PJ, Cracco RQ. Modelling magnetic coil excitation of human cerebral cortex with a peripheral nerve immersed in a brain-shaped volume conductor: the significance of fiber bending in excitation. Electroenceph Clin Neurophysiol. (1992) 85:291–301.
56. Maccabee PJ, Amassian VE, Cracco RQ, Cadwell JA. An analysis of peripheral motor nerve stimulation in humans using the magnetic coil. Electroenceph Clin Neurophysiol. (1988) 70:524–33.
57. Maccabee PJ, Eberle L, Amassian VE, Cracco RQ, Rudell A, Jayachandra M. Spatial distribution of the electric field induced in volume by round and figure ‘8’ magnetic coils: Relevance to activation of sensory nerve fibers. Electroenceph Clin Neurophysiol. (1990) 76:131–41.
58. Maccabee PJ, Amassian VE, Cracco RQ, Cracco JB, Eberle L, Rudell A. Stimulation of the human nervous system using the magnetic coil. J Clin Neurophysiol. (1991) 8:38–55.
59. Maccabee PJ, Amassian VE, Eberle LP, Rudell AP, Cracco RQ, Lai KS, et al. Measurement of the electric field induced into inhomogeneous volume conductors by magnetic coils: application to human spinal neurogeometry. Electroenceph Clin Neurophysiol. (1991) 81:224–37.
60. Ruohonen J, Panizza M, Nilsson J, Ravazzani P, Grandori F, Tognola G. Transverse-field activation mechanism in magnetic stimulation of peripheral nerves. Electroenceph Clin Neurophysiol. (1996) 101:167–74.
61. Schnabel V, Struijk JJ. Magnetic and electrical stimulation of undulating nerve fibres: a simulation study. Med Biol Eng Comput. (1999) 37:704–9.
62. Roth BJ, Maccabee PJ, Eberle L, Amassian VE, Hallett M, Cadwell J, et al. In-vitro evaluation of a four-leaf coil design for magnetic stimulation of peripheral nerve. Electroenceph Clin Neurophysiol. (1994) 93:68–74.
63. Roth Y, Zangen A, Hallett M. A coil design for transcranial magnetic stimulation of deep brain regions. J Clin Neurophysiol. (2002) 19:361–70.
64. Zangen A, Roth Y, Voller B, Hallett M. Transcranial magnetic stimulation of deep brain regions: Evidence for efficacy of the H-coil. Clin Neurophysiol. (2005) 116:775–9.
65. Roth BJ, Momen S, Turner R. Algorithm for the design of magnetic stimulation coils. Med Biol Eng Comput. (1994) 32:214–6.
66. Ren C, Tarjan PP, Popovic DB. A novel electric design for electromagnetic stimulation: the Slinky coil. IEEE Trans Biomed Eng. (1995) 42:918–25.
67. Kraus KH, Gugino LD, Levy WJ, Cadwell J, Roth BJ. The use of a cap-shaped coil for transcranial magnetic stimulation of the motor cortex. J Clin Neurophysiol. (1993) 10:353–62.
68. Lontis ER, Voigt M, Struijk JJ. Focality assessment in transcranial magnetic stimulation with double and cone coils. J Clin Neurophysiol. (2006) 23:463–72.
69. Ruohonen J, Ravazzani P, Grandori F, Ilmoniemi RJ. Theory of multichannel magnetic stimulation: Toward functional neuromuscular rehabilitation. IEEE Trans Biomed Eng. (1999) 46:646–51.
70. Ueno S, Sekino M. Figure-eight coils for magnetic stimulation: from focal stimulation to deep stimulation. Front Hum Neurosci. (2021) 15:805971. doi: 10.3389/fnhum.2021.805971
71. Lee SW, Fallegger F, Casse BDF, Fried SI. Implantable microcoils for intracortical magnetic stimulation. Sci Adv. (2016) 2:e1600889.
72. Davey K, Epstein CM. Magnetic stimulation coil and circuit design. IEEE Trans Biomed Eng. (2000) 47:1493–9.
73. Panizza M, Nilsson J, Roth BJ, Basser PJ, Hallett M. Relevance of stimulus duration for activation of motor and sensory fibers: Implications for the study of H-reflexes and magnetic stimulation. Electroenceph Clin Neurophysiol. (1992) 85:22–9.
74. Wassermann EM. Risk and safety of repetitive transcranial magnetic stimulation: report and suggested guidelines from the international workshop on the safety of repetitive transcranial magnetic stimulation, 5–7, 1996. Electroenceph Clin Neurophysiol. (1998) 108:1–16.
75. Rossi S, Hallett M, Rossini PM, Pascual-Leone A. The Safety of TMS Consensus Group (2009). Safety, ethical considerations, and application guidelines for the use of transcranial magnetic stimulation in clinical practice and research. Clin Neurophysiol. (2009) 120:2008–39.
76. Counter SA, Borg E, Lofqvist L. Acoustic trauma in extracranial magnetic brain stimulation. Electroenceph Clin Neurophysiol. (1991) 78:173–84.
77. Pascual-Leone A, Dhuna A, Roth BJ, Cohen L, Hallett M. Risk of burns during rapid-rate magnetic stimulation in presence of electrodes. Lancet. (1990) 336:1195–6.
78. Roth BJ, Pascual-Leone A, Cohen LG, Hallett M. The heating of metal electrodes during rapid-rate magnetic stimulation: a possible safety hazard. Electroenceph Clin Neurophysiol. (1992) 85:116–23.
79. Roth BJ. Mechanisms for electrical stimulation of excitable tissue. Crit Rev Biomed Eng. (1994) 22:253–305.
80. George MS, Wassermann EM, Williams WA, Callahan A, Ketter TA, Basser P, et al. Daily repetitive transcranial magnetic stimulation (rTMS) improves mood in depression. Neuroreport. (1995) 6:1853–6.