1. Introduction
Over the years, significant research efforts have been devoted to metal/oxide/semiconductor (MOS) structures to improve their reliability and understand their electronic and electric properties (1–9). One crucial aspect of this research is the use of high-k dielectric materials (high dielectric permittivity ε) in MOS structures, which plays a vital role in various applications. These materials must exhibit thermodynamic stability in direct contact with the semiconductor, possess a reasonable dielectric constant, and exhibit low tunneling current characteristics to be considered effective in MOS structures (10). Among the various conduction mechanisms observed in MOS structures, including tunneling currents (e.g., Fowler-Nordheim current), Schottky currents, space charge-limited currents, and Poole-Frenkel (PF) currents (11), understanding which current dominates and in what voltage interval is essential for optimizing device performance. The nature of the dominant current depends on the application domain of the device and it needs a detailed investigation of the causes that make it dominant compared to other current processes. In some applications, like high-fabricated electronic devices, the minimization of leakage currents such as the Poole-Frenkel one, and the causes that make it dominant is of great importance. This study considers defects and other factors that may affect the PF current, causing a significant improvement in the device’s performance and reliability. Our analysis emphasises on the effects of leakage currents, such as the PF current in MOS structures, by extracting the parameters that characterize this conduction mechanism.
Silicon dioxide (SiO2) is a key material in electronic and optical devices (12, 13) because of its excellent dielectric properties, transparency in the visible spectrum, and chemical stability. The elaboration methods for SiO2 are well-known and extensively used in the industry (14). Even though there are many dielectric materials that could offer advantages better than SiO2 for particular applications, like higher dielectric constants or lower leakage currents, the high compatibility between Si and SiO2 makes silicon dioxide a perfect choice in many applications (1). It is noteworthy that despite these remarkable advantages, using SiO2 as a gate oxide on a Si substrate (14) still poses challenges in elaboration, including, for example, the uniform thickness and quality of the oxide layer leading to control the interface states and minimize defects that can enhance the device’s performance (15–21). Accordingly, these challenges necessitate a deep understanding of the SiO2/Si interface and other factors that influence oxide growth and quality. By means of a deeper analysis of the PF current, we may improve the reliability and performance of MOS structures in several applications. In this investigation, we elaborated on a conventional MOS structure using aluminum (Al) as the gate contact. This gate was deposited on the silicon dioxide (SiO2) gate layer, which was also deposited on the silicon (Si) substrate. To create physical damage and generate traps near the gate electrode, a layer of titanium nitride (TiN) was introduced. This procedure conducts to the formation of defects within the SiO2 oxide, which in turn induces various current mechanisms. Therefore a considerable increase in the leakage currents (like the PF) is obtained. Our aim was to characterize this MOS structure using the current-voltage (I-V) measurement as a function of temperature, giving us the possibility to investigate the different parameters that influence the Poole-Frenkel conduction mechanism within this MOS structure. From this investigation, one could understand how the defects influence the leakage currents and the other parameters that characterize the electrical behavior of the MOS structure. The presence of the TiN layer and the resulting traps give the opportunity to study the PF currents systematically in a controlled manner. These findings are of great interest for improving the design and performance of MOS structures, mainly in applications where leakage currents play a critical role. The study underscores the importance of controlled defect introduction and its implications on the electrical properties of MOS devices.
The main innovation in our study lies in simultaneously extracting the five characterized parameters and modeling the PF current mechanism. Unlike other methods, such as capacitance-voltage (CV) measurements or graphical techniques, our approach does not rely on these for parameter extraction. The only measurement we require is the I-V-T curves of the MOS device.
2. Theoretical back ground
In a dielectric material (i.e., amorphous solids: oxides), different current mechanisms exist at the same time with different domination percentages. One of them, very frequently used to explain a part of the current mechanism, is the Poole-Frenkel current. The PF (22, 23) current is due to the emission of the trapped charge carriers from the trap center, permitting an electron to escape to the conduction band or a hole to outflow from the valence band of the oxide (24). The charge carriers are thermally exited and enhanced by the application of an external electric field, which will allow them to overcome the high barrier formed by these traps. This mechanism is also known as field-assisted emission. The current density J as a function of the applied electric field E in the Poole-Frenkel mechanism is given by Eq. (1) (24).
q is the elemental electric charge, Nh/e is the density of states of the charge carriers in the valence/conduction band: Nh/e = Nc (or Ne) if the charge carriers are electrons and Nh/e = Nv (or Nh) if the charge carriers are holes, μ is the charge carrier’s mobility, Vg is the applied voltage at the gate, ϕ is the barrier height that defines the position of the trap energy level, ε0 is the vacuum permittivity, εr is the relative permittivity of the material, k is the Boltzmann constant, and dox is the thickness of the oxide.
The electric field in the oxide is given by (25):
Vox is the voltage across the oxide.
After the correction of the voltage across the oxide (Vox), taking into account its dependence on the gate bias (Vg), the flat band voltage (VFB), and the surface potential (ψS), one will get (25):
Vcorr represents the correction of the oxide voltage; it depends on the flat band voltage and the surface potential, which both depend on temperature (26).
The sign of the voltage correction Vcorr is related to the type of semiconductor (p-type or n-type) and to the bias mode (accumulation or inversion). If the semiconductor is a p-type and it is biased in accumulation (Vg < 0), so the PF current is caused by the majority of charge carriers, which are the holes, and consequently, the relevant oxide voltage is given by Eq. (4). But if it is biased in inversion (Vg > 0), the PF current is caused by the minority charge carriers, which are the electrons, and the oxide voltage in this case is given by Eq. (5).
Substituting Eq. (3) in Eq. (1), we get:
In several studies (27–29), to determine some physical parameters like the relative permittivity εr using the current-voltage measurements, the graphical method is the most used one, where the PF plot (in which ln(I/V) is plotted as a function of) is showing a straight line variation. From the slope, one can determine the value of the relative permittivity εr, and from the intersection, the barrier high ϕ (formed by the traps in the oxide) could be obtained. However, to calculate the other parameters, we need other data, like, for example, CV measurements, to determine the flat band voltage VFB. From all those methods, we have to calculate the slopes and the intercepts from the graphical method to, after that, determine the other characterized parameters.
To extract simultaneously the different physical parameters (ϕ, Nh/e, μ, εr, and Vcorr) that model the Poole-Frenkel current from Eq. (2) without any previous calculations, approximations, or additional measurements, we use the so-called vertical optimization method (VOM). This method is based on the optimization of the parameter’s vector (ϕ, Nh/e, μ, εr, and Vcorr) modeling the current-voltage measurements (30). The optimization criterion is used on the vertical axis, which is the current. We have to fit the experimental current-voltage curves as a function of the temperature (I-V-T) with the I-V-T curves calculated with the extracted parameters and then minimize the associated vertical quadratic error S defined by Eq. (7).
N is the number of measured points, Iimeasured and Iitheoretical are the ith measured current and fitting value of the current, respectively.
To fulfill the optimization condition, we have to solve a system of equations with n degree, depending on the number of parameters to extract. In our study, we have to extract (ϕ, Nh/e, μ, εr, and Vcorr), thus n = 5, and the system to be resolved is presented in Eq. (2).
3. Experimental details
A conventional MOS structure with silicon dioxide (SiO2) as a dielectric material and silicon (Si) as a substrate semiconductor (1–6 Ωcm) was prepared. The oxide with a thickness of 9 nm has been deposited on p-type Si by the dry oxidation technique. After that, a gate of 104μm2 was deposited on the oxide, containing 20 nm of titanium nitride (TiN) layer and 300 nm of aluminum (Al) stacks. They were elaborated with plasma sputtering and patterned via photolithography and dry etching, respectively. The MOS structure was annealed with a forming gas annealing at 430°C for 30 min. The TiN layer was deposited intentionally to create defects in the oxide and allow other current mechanisms to exist. The current-voltage measurements (I-V) in inversion and accumulation mode are done with a semiconductor parameter analyzer (HP 4156 A). To investigate deeply the conduction mechanism in the fabricated MOS structure, we have measured the I-V in both modes in the temperature range of 303–423 K.
4. Experimental current-voltage curves
The current density J of the investigated MOS structure described earlier as a function of the applied voltage in the range of temperature 303–423 K is shown in Figure 1a, b for the accumulation and the inversion mode, respectively. The related energy band diagram of the investigated MOS structure is illustrated in Figure 1c. To extract simultaneously the set vector of the parameters that characterize the PF conduction mechanism described by Eq. (2), we have used the vertical optimization method detailed by Eq. (8). To validate the reliability of the extracted parameters, we compare the measured (I-V-T) data for the studied MOS structure with the (I-V-T) curves calculated with the PF parameters (ϕ, Nh/e, μ, εr, and Vcorr) extracted simultaneously with the VOM. Figure 2a, b illustrates the measured (I-V-T) curves in comparison with those calculated by the extracted parameters for accumulation and inversion mode, respectively. We remark that for the same temperature, a remarkable alignment between the experimental and calculated curves is achieved.

Figure 1. Experimental current-voltage characteristics of TiN/Al/SiO2/p-Si MOS structure in the temperature range of 303–423 K: (a) biased in accumulation mode, (b) biased in inversion mode, (c) Energy band diagram of the investigated MOS structure.

Figure 2. Experimental (as characters) and calculated (as dashed lines) current-voltage characteristics of the TiN/Al/SiO2/p-Si MOS structure at different temperatures. Calculations are done by means of Eq. (2) using the extracted parameters by the vertical optimization method (VOM): (a) accumulation mode, (b) inversion mode.
5. Temperature effect on the five extracted parameters in the TiN/Al/SiO2/p-type Si structure
5.1. Temperature-dependent barrier ϕ (T)
Analyzing the impact of temperature on the extracted parameters allows a thorough investigation of the conduction mechanism and its susceptibility to temperature variation. To evaluate the temperature’s influence on the position of the traps in terms of energy in the oxide, we have extracted the values of the barrier high ϕ for the range temperature of 303–423 K with the PF mechanism as a conduction process. The temperature dependence of the barrier ϕ for the studied MOS structure biased in accumulation mode is illustrated in Figure 3. The barrier ϕ decreases with the increase in temperature. The same variation of the barrier ϕ is observed when the MOS is biased in inversion mode as shown in Figure 4. To model the obtained values of the barrier ϕ in the 303–423 K temperature range, we fit the ϕ(T) variation with a linear model. The linear fit gives slopes of dϕ/dT = −1.16 meV/K and dϕ/dT = −0.833 meV/K and intercepts equal to 3.07 eV and 3.45 eV for the accumulation and the inversion modes, respectively. It is noteworthy that the decrease of ϕ with the increase of T in the accumulation mode is more important than that in the inversion mode. In the accumulation mode, the barrier ϕ represents the position of the traps in terms of energy compared to the valence band EV, which means that the charge carrier (hole in this case) is escaping from the traps to the valence band to form the PF current. However, in the inversion mode, the barrier ϕ also represents the position of the traps in terms of energy, but compared to the conduction band EC, which means that the charge carrier (an electron in this case) is escaping from the traps to the conduction band to form the PF current. From the linear model, when the temperature increases, ϕ decreases significantly for the accumulation mode than for the inversion mode; consequently, the traps are more controlled and could be surmounted to generate the PF current when the MOS structure is biased in accumulation with holes as charge carriers than when it is biased in inversion with electrons as charge carriers. One could get from the intercepts of the linear regression modeling ϕ(T) the values of the trap’s energy at T = 0 K for the holes and the electrons in the studied MOS structure. ϕ(T = 0 K) is found to be equal to 3.074 eV for the holes in the accumulation mode and to 3.459 eV for electrons in the inversion mode. The obtained values of ϕ at T = 0 K confirm that the traps in the two regions are deep [ϕ > 3 eV (31)], but the traps for electrons are deeper than those for holes, as shown earlier. The rise of the temperature affects the variation by reducing the barrier’s values, with Δϕacc = ϕ423 K-ϕ303 K = 0.13 eV and Δϕinv = ϕ423 K-ϕ303 K = 0.1 eV in the accumulation and inversion modes, respectively. We can also remark that even when the temperature reaches the value of 423 K the traps are stable (ϕ ¿ 3eV) for the inversion mode. However, in the accumulation mode, the trap level starts to be reduced remarkably. This result means that when the MOS structure is biased in inversion, the PF mechanism does not contribute notably because the traps stay stable with a barrier more than 3 eV. K. Murakami et al. (32) have investigated the same MOS structure and have reported that for the inversion mode, the PF emission is not the dominant mechanism, which is in good agreement with the present results. In addition to all the above results, we are able to localize the position of traps for electrons and holes in the forbidden region of the used oxide (SiO2: Eg = 8.6 eV) (33) in comparison with the conduction band EC/valence band EV.

Figure 3. Temperature dependencies of the barrier ϕ for the studied MOS structure biased in accumulation mode.

Figure 4. Variation of the barrier ϕ as a function of temperature for the TiN/Al/SiO2/p-Si MOS structure biased in inversion mode.
5.2. Densities of charge carriers dependencies Nh/e(T)
The parameter Nh/e indicates the density of the charge carriers responsible for the PF current in the oxide. In the accumulation mode, the PF current originates from the holes as the charge carriers. However, in the inversion mode, the electrons are considered as the charge carriers. The effect of temperature on the density of holes Nh in the accumulation mode and on the density of electrons Ne in the inversion mode are represented in Figures 5 and 6, respectively. The figures show a decrease in the densities of carriers (Nh, Ne) in both modes as the temperature rises. The densities Nh(T) and Ne(T) vary in the range of 7 × 1018–5 × 1010 cm−3 and 6.5 × 1018–7.98 × 1016 cm−3 when the MOS structure is biased in accumulation and inversion, respectively. The temperature dependences of the densities Nh and Ne for both modes are confirmed by the ϕ(T) behavior discussed earlier and indicate that for the accumulation mode, the PF current mechanism is more pronounced than that for the inversion one.

Figure 6. The electron density Ne(T) variation for the TiN/Al/SiO2/p-Si MOS structure biased in inversion.
5.3. Temperature effect on charges mobilities μh/e(T)
Another important parameter under investigation in this study, which characterizes the current conduction mechanism within the oxide, is the charge carriers’ mobility μ. We analyze how the charge carrier responsible for the current mechanism is affected by the variation in temperature. Since our MOS structures are biased in two modes, we distinguish two types of the charge carrier’s mobility: the hole mobility μh for the accumulation mode and the electron mobility μe for the inversion mode. The temperature dependencies of the (μh and μe) for the studied MOS structure in the temperature range of 303–423 K are illustrated in Figures 7a and 8a, respectively. Both (μh and μe) decrease when the temperature increases. The decrease in the mobility of the charge carrier with the increase in the temperature is expected for oxides at temperatures >150 K (34, 35). However, it should be noted that even when the temperature is elevated to 363 K, the mobility for holes stays considerable (1010 cm2/Vs) compared to that of electrons (2.7 × 109 cm2/Vs). These results affirm that the PF leakage current issued from holes is more prevalent in the studied MOS structure compared to the current issued from electrons at elevated temperatures.

Figure 7. (a) Temperature dependence of hole mobility for the TiN/Al/SiO2/p-Si MOS structure. (b) An Arrhenius fit to the data gives μh = 0.48 × 10−9exp(+ 1.413eV/kT) cm2/Vs.
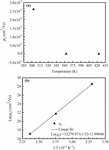
Figure 8. (a) Temperature dependence of electron mobility for the TiN/Al/SiO2/p-Si MOS structure. (b) An Arrhenius fit to the data gives μe = 0.62 × 10−5exp(+ 1.0639eV/kT) cm2/Vs.
The notably high hole/electron mobility values, extracted from the measured I-V curves even at room temperature, can likely be attributed to the presence of the 20 nm TiN layer, which creates defects. As reported by T. Koida et al. (36), the existence of these defects can lead to a remarkable increase in mobility. Then, as shown in Figures 7a and 8a the mobility of the charge carriers decreases gradually with the increase in temperature because of the inverse proportional relationship between mobility and temperature. However, for extreme high temperatures, the mobility of holes becomes very low compared to that of electrons, as shown when an Arrhenius fit (Figures 7b and 8b) is used for the data from Figures 7a and 8a. It gives the mobilities of holes and electrons as charge carriers for very elevated temperatures (T→∞), which are equal to 0.48 × 10−9 cm2/Vs and 0.62 × 10−5 cm2/Vs for the accumulation and inversion modes, respectively. Accordingly, the studied MOS structure (SiO2 deposited on p-type Si) is suitable for applications at elevated temperatures when the charge carriers are electrons because the PF current mechanism is not significantly pronounced as reported by Vladimir P. Popov et al (37).
5.4. Relative permittivity dependencies εr(T)
The extraction of the relative permittivity εr for the studied MOS structure in the same range of temperature is shown in Figures 9 and 10 for the accumulation and inversion modes, respectively. The temperature dependency of εr shows a decrease when the temperature increases for both modes. Different power laws fits are used to fit the temperature dependency of the relative permittivity εr; however, the linear fit gives the minimum values of errors for both modes in the studied range of temperature. A linear fit to the εr(T) data gives slopes equal to dεr/dT = -18.61 × 10−3K−1 and dεr/dT = -10−3 K−1 for the accumulation and inversion modes, respectively. From the intersection of these linear fits, we can obtain the values of the εr at T = 0 K: for the accumulation mode, εr(T = 0 K) = 9.84 and for the inversion mode εr(T = 0 K) = 1.83.

Figure 9. Extracted values of the relative permittivity εr in temperature range of 303–423 K for the studied MOS biased in accumulation. A linear fit to the data gives εr(T = 0 K) = 9.84.

Figure 10. Permittivity εr versus temperature in inversion mode. A linear fit to the data gives εr(T = 0 K) = 1.83.
A. S. Konashuk et al. (38) have reported that one has to decrease the dielectric permittivity value (εr) of the insulating material to reduce the parasitic capacity issued from the rapprochement of the metallic lines in a denser microchip where the larger part of its cross-section becomes occupied by those metallic lines (39, 40). Many techniques are used to decrease the dielectric permittivity, but the ones that are already being used in the industry are including porosity into the structure of SiO2 or substituting some oxygen atoms by terminating –CH3 methyl groups (38). From the results found for the εr(T), the values of the dielectric permittivity are significantly reduced when increasing temperature for holes as charge carriers compared to the ones for electrons as charge carriers, thus, we could say that the increasing of the temperature of the MOS structure could be used as a technique to decrease the values of the dielectric permittivity of the oxide to be used for different technologies (in semiconductor integrated circuits) based on low εr dielectrics.
It is well known that the parameter εr of the dielectric material is directly related to its polarization. When the relative permittivity of the oxide (SiO2 in our case) rises, the dielectric becomes more polarized. From the εr(T) behavior of the studied MOS structure, the SiO2 becomes more polarized when the temperature decreases. Which means that the decrease in temperature makes the oxide more polarized in response to the applied voltage. According to the discussion in the following section of the temperature dependency of the relative permittivity, the dielectric properties of the SiO2 oxide in terms of polarization properties are more pronounced when the MOS structure is biased in accumulation than in inversion.
5.5. Temperature dependencies of the oxide voltage Vcorr(T)
The effect of temperature on the oxide voltage correction Vcorr in the accumulation mode is represented in Figure 11. For the inversion mode, the variation of Vcorr as a function of temperature is shown in Figure 12. When the MOS structure is biased in accumulation, the extracted values of Vcorr decrease with the increase in temperature. The variation of the oxide voltage correction in the temperature range 303–423 K is equal to ΔVcorr−acc = Vcorr(423K)–Vcorr(303K) = −1.33 V. However, it increases with the increase in temperature when the MOS structure is biased in inversion. This variation is equal to ΔVcorr−inv = Vcorr(423K)–Vcorr(303K) = 1.03 V for the same range of temperature. To model the effect of temperature on Vcorr(T) for both modes, we propose a linear fitting for the extracted values of the voltage Vcorr. The slopes of these linear regressions are dVcorr/dT = −5.09 mV/K and dVcorr/dT = 8.58 mV/K for the accumulation and inversion modes, respectively. From the intercepts, we can have the values of the oxide voltage correction at T = 0 K for holes as charge carriers in the accumulation mode and for electrons as charge carriers in the inversion mode. They are equal to 2.606 V and −2.302 V in the accumulation and inversion modes, respectively.

Figure 11. Temperature dependences of the oxide voltage correction Vcorr for the TiN/Al/SiO2/p-Si MOS structure biased in accumulation. A linear fit to the extracted values of Vcorr gives Vcorr(T = 0 K) = 2.606 V with a slope of dVcorr/dT = –5.09 mV/K.

Figure 12. Variation of the extracted values of the voltage Vcorr as a function of temperature in inversion mode. A linear fit to the data gives Vcorr(T = 0 K) = –2.302 V and a slope of dVcorr/dT = 8.58 mV/K.
It is well known that for T = 0 K, the structure operates within the flat band regime, so, Vcorr(T = 0 K) = VFB = 2.606 V and Vcorr(T = 0 K) = VFB = −2.302 V for the accumulation and the inversion modes, respectively.
However, the flat band potential depends on temperature, as indicated in Eq. (9) (41).
T0 is the room temperature, and VFB0 is the flat band voltage at T0.
Taking into account the linear variation of Vcorr [the value of Vcorr(T = 0 K)] and the Eq. (9) for the flat band regime, the final values of the oxide voltage correction at T = 0 K are as shown in Eq. (10) and (11) for accumulation and inversion modes, respectively.
The obtained values are the flat band potential at T = 0 K for the Poole-Frenkel mechanism, representing the placement of the band levels between the oxide and the semiconductor when it is biased in accumulation and inversion.
By analyzing the measured current-voltage curves as a function of temperature (I-V-T), we could simultaneously determine the characterized parameters of the Poole-Frenkel conduction mechanism and investigate how the temperature affects these parameters.
6. Conclusion
In this work, we have investigated the Al/SiO2/p-type Si MOS structure in the temperature range of 303–423 K. The traps in the oxide have been intentionally created by depositing a 20 nm TiN layer. The analysis of the charge carrier’s current in the studied MOS structure as a function of temperature was described by the PF current mechanism. The investigation reported on the simultaneous extraction of the five parameters (ϕ, Nh/e, μ, εr, and Vcorr) that characterize the PF current conduction process as a function of temperature utilizing the VOM. The temperature-dependent variation of the barrier ϕ in both modes shows the same behavior. It decreases with an increase in temperature. We have fitted the ϕ(T) variation with a linear model, which gives slopes of dϕ/dT = −1.16 meV/K and dϕ/dT = −0.833 meV/K and intercepts equal to 3.07 eV and 3.45 eV for the accumulation and the inversion modes, respectively. The temperature dependence of the barrier ϕ in both modes affirms that the traps for electrons are deeper than those for holes. A decrease in the densities of carriers (Nh and Ne) in both modes as the temperature rises have been observed. The densities Nh(T) and Ne(T) vary in the range of 7 × 1018–5 × 1010 cm−3 and 6.5 × 1018–7.98 × 1016 cm−3 when the MOS structure is biased in accumulation and inversion, respectively. The temperature dependences of the densities Nh and Ne for both modes are confirmed by the ϕ(T) behavior discussed earlier and indicate that for the accumulation mode, the PF current mechanism is more pronounced than that for the inversion one. The variation of the hole/electron mobilities (μh, μe) as a function of T for the studied MOS indicates that even at elevated temperatures up to 363 K, hole mobility remains considerable (1010 cm2/Vs) compared to electron mobility (2.7 × 109 cm2/Vs). But for very high temperatures, the hole mobility becomes very low (= 0.48 × 10−9 cm2/Vs), whereas the electron mobility remains higher (= 0.62 × 10−5 cm2/Vs) as shown by an Arrhenius fit to the extracted values of μh and μe. From the relative permittivity εr(T) behavior of the studied MOS structure, the εr shows a decrease when the temperature increases for both modes. A linear fit to the εr(T) data gives slopes equal to dεr/dT = −18.61 × 10−3 K−1 and dεr/dT = −10−3 K−1 for the accumulation and inversion modes, respectively. From the intersection of these linear fits, we can obtain the values of the εr at T = 0 K for the accumulation mode εr(T = 0 K) = 9.84 and for the inversion mode εr(T = 0 K) = 1.83. The εr(T) behavior of the studied MOS structure has shown that SiO2 becomes more polarized when the temperature decreases. Which means that the decrease in temperature makes the oxide more polarized in response to the applied voltage. Accordingly, the dielectric properties of the SiO2 oxide in terms of polarization properties are more pronounced when the MOS structure is biased in accumulation than in inversion. The voltage correction Vcorr included in the oxide voltage was analyzed as a function of temperature. In the accumulation mode, the extracted values of Vcorr decrease with the increase in temperature, with ΔVcorr–acc = Vcorr(423 K)–Vcorr(303 K) = −1.33 V. However, it increases with the increase in temperature when the MOS structure is biased in inversion, with ΔVcorr–inv = Vcorr(423 K)–Vcorr(303 K) = 1.03 V. A linear fit has been used to model this behavior, giving slopes of dVcorr/dT = −5.09 mV/K and dVcorr/dT = 8.58 mV/K for the accumulation and inversion modes, respectively. The use of the intercepts could give us the oxide voltage correction at T = 0 K for holes (in accumulation) and for electrons (in inversion). They are equal to 2.606 V and −2.302 V in the accumulation and inversion modes, respectively.
Based on the results found in this work, we can deduce that the trapping and detrapping mechanisms are more important for holes in the accumulation mode than for electrons in the inversion mode for the investigated MOS structure in the temperature range of 303–423 K. Consequently, the p-type MOS with the PF mechanism as a leakage current is not suitable for technological applications. But the n-type MOS holds greater promise for such applications, even at elevated temperatures, because the leakage PF current mechanism is less pronounced.
Conflict of interest
The authors declare that the research reported in this work is not supported by any institutions or sources. Accordingly, the authors declare that they have no competing interests.
Author contributions
The individual contributions of the authors to the manuscript are as follows: S. Toumi: Wrote the paper, performed the analysis and the analysis tools, conceived and designed the analysis. Z. Ouennoughi: Collected the data.
Funding
The authors declare that the research reported in this work is not supported by any institutions or sources.
Acknowledgments
We would like to thank Pr. K. Murakami, chair of electron devices from the University of Erlangen-Nuremberg, Germany, for providing us with the current-voltage measurements as a function of temperature for the investigated MOS structures. One of the authors, S. Toumi, is very grateful to Pr. T. Guerfi from the Department of Physics, University of Boumerdes, for the valuable and fruitful discussions and for the correction of this manuscript.
References
1. Huff HR, Gilmer DC. High Dielectric Constant Materials. VLSI MOSFET Applications. Berlin: Springer-Verlag (2005).
2. El-Sayed A, Watkins MB, Afanas’ev VV, Shluger AL. Nature of intrinsic and extrinsic electron trapping in SiO2. Phys Rev B (2014) 89:125201.
3. Shih-Fang Chen C-. Effects of deposition temperature on the conduction mechanisms and reliability of radio frequency sputtered TiO2 thin films. J Vac Sci Technol B. (2002) 20(1):263–70.
4. Bonilla Ruy S, Wilshaw PR. On the c-Si/SiO2 interface recombination parameters from photo-conductance decay measurements. J Appl Phys. (2017) 121:135301.
5. Choueib M, Ayari PV, Perisanu S, Purcell ST. Evidence for Poole–Frenkel conduction in individual SiC nanowires by field emission transport measurements. J Appl Phys. (2011) 109:073709.
6. Pei Y, Yu S, Zuo X. First-Principles Calculations of Silicon Interstitial Defects at the Amorphous-SiO2/Si Interface. J. Phys. Chem. C (2021) 125(27):15044–51.
7. Han SW, Yun WS, Woo WJ, Kim H, Park J, Hun Hwang Y, et al. Interface Defect Engineering of a Large-Scale CVD-Grown MoS2 Monolayer via Residual Sodium at the SiO2/Si Substrate. Adv. Mater. Interfaces (2021) 8:2100428.
8. Ko E, Choi J. Comparison of interfaces, band alignments, and tunneling currents between crystalline and amorphous silica in Si/SiO2/Si structures. Mater. Res. Express (2022) 9:045005.
9. Li P, Chen Z, Yao P, Zhang F, Wang J, Song Y, et al. First-principles study of defects in amorphous-SiO2/Si interfaces. Appl Surf Sci. (2019) 483:231–40.
10. Kitai S, Maida O, Kanashima T, Okuyama M. Preparation and Characterization of High-k Praseodymium and Lanthanoid Oxide Thin Films Prepared by Pulsed Laser Deposition. Jpn. J. Appl. Phys. (2003) 42:247–53.
12. Islamov DR, Gritsenko VA, Perevalov TV, Orlov OM, Krasnikov GY. The charge transport mechanism and electron trap nature in thermal oxide on silicon. Appl. Phys. Lett. (2016) 109:052901.
13. Nekrashevich SS, Gritsenko VA. Electronic Structure of Silicon Dioxide (A Review). Physics of the Solid State (2014) 56(2):207–22.
15. DiMaria DJ, Cartier E, Arnold D. Impact ionization, trap creation, degradation, and breakdown in silicon dioxide films on silicon J. Appl. Phys. (1993) 73:3367–84.
16. DiMaria DJ, Arnold D, Cartier E. Degradation and breakdown of silicon dioxide films on silicon Appl. Phys. Lett. (1992) 61:2329–31.
17. Apte PP, Saraswat C. Correlation of trap generation to charge-to-breakdown (q/sub bd/): a physical-damage model of dielectric breakdown IEEE Trans. Electron Devices. (1994) 41:1595–602.
18. Dumin DJ, Maddux JR, Scott RS, Subramoniam R. A model relating wear out to breakdown in thin oxides IEEE Trans. Electron Devices. (1994) 41:1570–80.
19. Lodh S, Chakraborty R, Das A. Effect of atomic layer deposited ultra-thin SiO2 layer on vapour-liquid-solid (VLS) grown high dielectric TiO2 film for Si-based MOS device applications. Micro Nano Lett. (2021) 16:71–6.
20. Wilhelmer C, Waldhoer D, Jech M, Bellah El-Sayed A, Cvitkovich L, Waltl M, et al. Ab initio investigations in amorphous silicon dioxide: Proposing a multi-state defect model for electron and hole capture. Microelectron Reliabil. (2022) 139:114801.
21. Matsumoto N, Takao Y, Nagao M, Murakami K. Oxidation Resistance Improvement of Graphene-Oxide-Semiconductor Planar-Type Electron Sources Using h-BN as an Oxygen-Resistant Electron-Transmissive Coating. ACS Omega. (2022) 7:33004–9.
22. Poole HH. On the Temperature Variation of the JElectrical Conductivity of Mica. Philosophical Magazine Series. (1917) 201:195–204.
23. Frhnkel J. On Pre-Breakdown Phenomena in Insulators and Electronic Semi-Conductors. Phys. Rev. (1938) 54:647–8.
24. Jimenez MJ, de Oliveira RF, Shimizu FM, Bufon CC, Rodrigues V, Gobbi AL, et al. Poole–Frenkel emission on functionalized, multilayered-packed reduced graphene oxide nanoplatelets. Nanotechnology. (2018) 29:505703.
25. Toumi S, Ouennoughi Z, Murakami K. Effect of temperature on the Fowler-Nordheim barrier height, flat band potentials and electron/hole effective masses in the MOS capacitors. Physica B (2020) 585:412125.
26. Hadjadj A, Salace G, Petit C. Fowler–Nordheim conduction in polysilicon (n+)-oxide-silicon (p) structures: Limit of the classical treatment in the barrier height determination. J. Appl. Phys. (2001) 89(12):7994–8001.
27. Cheong KY, Lockman Z, Aziz A, Moon JH, Kim HJ, Bahng W, et al. Current conduction mechanisms of atomic-layer-deposited Al2O3/nitrided SiO2 stacking gate oxide on 4H-Si. Int J Modern Phys B. (2010) 24(27):5371–8.
28. Koteswara Rao P, Park B, Lee S, Noh Y, Kim M. Analysis of leakage current mechanisms in Pt/Au Schottky contact on Ga-polarity GaN by Frenkel-Poole emission and deep level studies. Journal of Applied Physics (2011) 110:013716.
29. Arslan E, Bütün S, Ozbay E. Leakage current by Frenkel–Poole emission in Ni/Au Schottky contacts on Al0.83In0.17N/AlN/GaN heterostructures. Appl Phys Lett. (2009) 94:142106.
30. Ortiz-Conde A, Yuansheng, Ma, Thomson J, Santos E, Liou JJ, et al. Direct extraction of semiconductor device parameters using lateral optimization method. Solid-State Electronics. (1999) 43(4):845–8.
31. Martinez-Vega J. Dielectric Materials for Electrical Engineering. London: John Wiley & Sons, Inc (2010).
32. Murakami K, Rommel M, Yanev V, Erlbacher T, Bauer AJ, Frey L. A highly sensitive evaluation method for the determination of different current conduction mechanisms through dielectric layers. J Appl Phys. (2011) 110:054104.
33. Yang J, Kim W, Park H. Chemical bonding states and energy band gap of SiO2-incorporated La2O3 films on n-GaAs (001). Thin Solid Films. (2006) 494:311–4.
34. Trier F, Christensen DV, Pryds N. Electron Mobility in Oxide Heterostructures. J. Phys. D: Appl. Phys. (2018) 51:293002.
35. Hughes RC. Hole mobility and transport in thin SiO2 films. Appl Phys Letters. (1975) 26(8):436–8.
36. Koida T, Ueno Y, Shibata H. In2O3-Based Transparent Conducting Oxide Films with High Electron Mobility Fabricated at Low Process Temperatures. Phys. Status Solidi A (2018):17005061–170050614.
37. Popov VP, Antonov VA, Miakonkikh AV, Rudenko KV. Ion Drift and Polarization in Thin SiO2 and HfO2 Layers Inserted in Silicon on Sapphire. Nanomaterials (2022) 12:3394.
38. Konashuk AS, Filatova EO. Redistribution of valence and conduction band states depending on the method of modification of SiO2 structure. Phys.Chem.Chem.Phys. (2017) 19:26203–9.
39. Grill A, Gates SM, Ryan TE, Nguyen SV, Priyadarshini D. Progress in the development and understanding of advanced low k and ultralow k dielectrics for very large-scale integrated interconnects—State of the art. Appl. Phys. Rev. (2014) 1:011306.
40. Maex K, Baklanov MR, Shamiryan D, Iacopi F, Brongersma SH, Yanovitskaya ZS. Low dielectric constant materials for microelectronics.J. Appl. Phys. (2003) 93(11):8793–841.
41. Waters R, Zeghbroeck BV. Temperature-dependent tunneling through thermally grown SiO2 on n-type 4H- and 6H-SiC. Appl. Phys. Lett. (2000) 76(8):1039–41.
© The Author(s). 2024 Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
